如图,平面ABCD⊥平面ADEF,其中ABCD为矩形,ADEF为梯形,AF∥DE,AF⊥FE,AF=AD=2DE=2.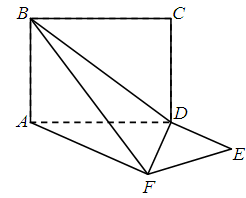
(Ⅰ)求异面直线EF与BC所成角的大小;
(Ⅱ)若二面角A-BF-D的平面角的余弦值为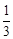 ,求AB的长.
,求AB的长.
(本小题满分l2分)已知{an}的前n项和 (其中
(其中 ),且Sn的最大值为9。
),且Sn的最大值为9。
(1)确定常数k的值,并求数列{an}的通项公式;
(2)求数列 的前n项和
的前n项和 。
。
(本小题满分12分)已知函数 在区间[2,3]上有最大值4和最小值1.设
在区间[2,3]上有最大值4和最小值1.设 .
.
(1)求a、b的值;
(2)若不等式 上有解,求实数k的取值范围。
上有解,求实数k的取值范围。
已知函数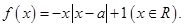
(Ⅰ)当 时,求使
时,求使 成立的
成立的 的值;
的值;
(Ⅱ)当 ,求函数
,求函数 在
在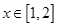 上的最大值;
上的最大值;
(Ⅲ)对于给定的正数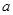 ,有一个最大的正数
,有一个最大的正数 ,使
,使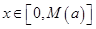 时,都有
时,都有 ,试求出这个正数
,试求出这个正数 ,并求它的取值范围.
,并求它的取值范围.
设向量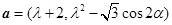 ,
,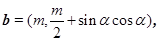 其中
其中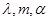 为实数.
为实数.
(Ⅰ)若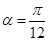 ,且
,且 求
求 的取值范围;
的取值范围;
(Ⅱ)若 求
求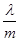 的取值范围.
的取值范围.
已知数列 的前
的前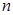 项和
项和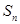 满足
满足
 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设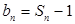 ,且数列
,且数列 为等比数列.
为等比数列.
①求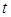 的值;
的值;
②若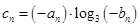 ,求数列
,求数列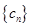 的前
的前 和
和 .
.