如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD丄CD,AB//CD,AB=AD= CD=2,点M在线段EC上.
CD=2,点M在线段EC上.
(I)当点M为EC中点时,求证: 面
面 ;
;
(II)求证:平面BDE丄平面BEC;
(III)若平面说BDM与平面ABF所成二面角锐角,且该二面角的余弦值为 时,求三棱锥M-BDE的体积.
时,求三棱锥M-BDE的体积.
(本小题满分12分)设函数 .
.
(1)若函数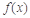 在
在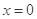 处有极值,求函数
处有极值,求函数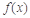 的最大值;
的最大值;
(2)①是否存在实数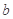 ,使得关于
,使得关于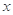 的不等式
的不等式 在
在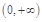 上恒成立?若存在,求出
上恒成立?若存在,求出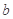 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
②证明:不等式
(本小题满分12分)设函数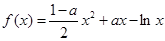 (
(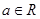 ).
).
(1)当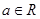 时,讨论函数
时,讨论函数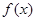 的单调性;
的单调性;
(2)若对任意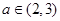 及任意
及任意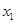 ,
,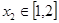 ,恒有
,恒有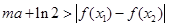 成立,求实数
成立,求实数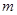 的取值范围.
的取值范围.
(本小题满分12分) 已知函数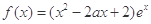 .
.
(Ⅰ)函数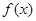 在
在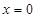 处的切线方程为
处的切线方程为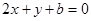 ,求a、b的值;
,求a、b的值;
(Ⅱ)当 时,若曲线
时,若曲线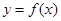 上存在三条斜率为k的切线,求实数k的取值范围.
上存在三条斜率为k的切线,求实数k的取值范围.
(本小题满分12分)
已知函数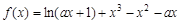
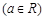 .
.
(1)若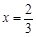 为函数
为函数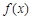 的极值点,求实数
的极值点,求实数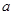 的值;
的值;
(2)若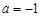 时,方程
时,方程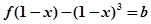 有实数根,求实数
有实数根,求实数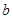 的取值范围.
的取值范围.
(本小题满分12分)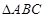 中,角
中,角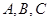 的对边分别为
的对边分别为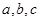 ,已知点
,已知点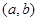 在直线
在直线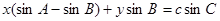 上.
上.
(1)求角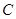 的大小;
的大小;
(2)若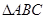 为锐角三角形且满足
为锐角三角形且满足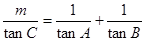 ,求实数
,求实数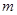 的最小值。
的最小值。