某学校900名学生在一次百米测试中,成绩全部介于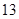 秒与
秒与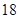 秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组
秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组 ,第二组
,第二组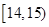 ,…,第五组
,…,第五组 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.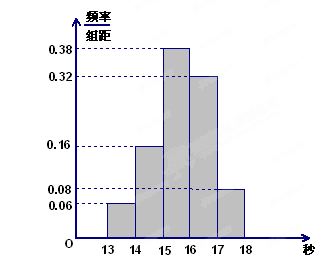
(1)若成绩小于14秒认为优秀,求该样本在这次百米测试中成绩优秀的人数;
(2)请估计学校900名学生中,成绩属于第四组的人数;
(3)请根据频率分布直方图,求样本数据的众数和中位数(保留两位小数).
已知函数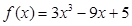 .
.
(Ⅰ)求函数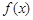 的单调递增区间;
的单调递增区间;
(Ⅱ)求函数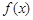 在
在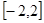 的最大值和最小值.
的最大值和最小值.
已知函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 在
在 处取得极小值
处取得极小值 。设
。设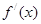 表示
表示 的导函数,定义数列
的导函数,定义数列 满足:
满足:
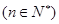
(Ⅰ)求数列 的通项公式
的通项公式 ;
;
(Ⅱ)对任意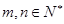 ,若
,若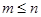 ,证明:
,证明: ;
;
(Ⅲ)(理科)试比较 与
与 的大小。
的大小。
已知焦点在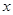 轴上椭圆的长轴的端点分别为
轴上椭圆的长轴的端点分别为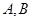 ,
,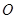 为椭圆的中心,
为椭圆的中心, 为右焦点,且
为右焦点,且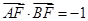 ,离心率
,离心率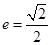 。
。
(Ⅰ)求椭圆的标准方程;
(Ⅱ)记椭圆的上顶点为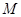 ,直线
,直线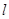 交椭圆于
交椭圆于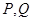 两点,问:是否存在直线
两点,问:是否存在直线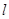 ,使点
,使点 恰好为
恰好为 的垂心?若存在,求出直线
的垂心?若存在,求出直线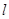 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。
已知数列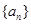 中,
中,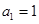 ,
,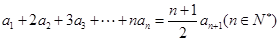
(Ⅰ)求数列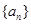 的通项公式;
的通项公式;
(Ⅱ)求数列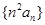 的前
的前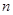 项和
项和 ;
;
(Ⅲ)(理科)若存在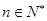 ,使得
,使得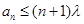 成立,求实数
成立,求实数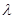 的最小值。
的最小值。
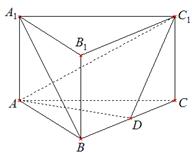
如图,在直三棱柱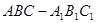 中,
中,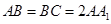 ,
, ,
, 是
是 的中点.
的中点.
(Ⅰ)求证: ∥平面
∥平面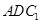 ;(Ⅱ)求二面角
;(Ⅱ)求二面角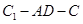 的余弦值;
的余弦值;
(Ⅲ)(理科)试问线段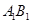 上是否存在点
上是否存在点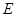 ,使
,使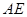 与
与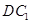 成
成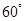 角?若存在,确定
角?若存在,确定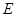 点位置,若不存在,说明理由.
点位置,若不存在,说明理由.