以平面上一点O为直角顶点,分别画出两个直角三角形,记作△AOB和△COD,其中∠ABO=∠DCO=30°.
(1)点E、F、M分别是AC、CD、DB的中点,连接EF和FM.
①如图1,当点D、C分别在AO、BO的延长线上时, =_______;
=_______;
②如图2,将图1中的△AOB绕点O沿顺时针方向旋转 角(
角( ),其他条件不变,判断
),其他条件不变,判断 的值是否发生变化,并对你的结论进行证明;
的值是否发生变化,并对你的结论进行证明;
(2)如图3,若BO= ,点N在线段OD上,且NO=3.点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.
,点N在线段OD上,且NO=3.点P是线段AB上的一个动点,在将△AOB绕点O旋转的过程中,线段PN长度的最小值为_______,最大值为_______.
如今很多初中生购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:
:自带白开水; :瓶装矿泉水; :碳酸饮料; :非碳酸饮料.
根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题:
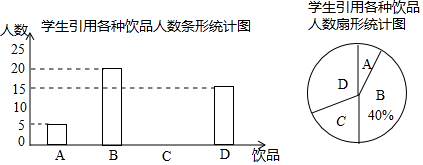
(1)这个班级有多少名同学?并补全条形统计图.
(2)若该班同学每人每天只饮用一种饮品(每种仅限1瓶,价格如下表),则该班同学用于饮品上的人均花费是多少元?
|
饮品名称 |
自带白开水 |
瓶装矿泉水 |
碳酸饮料 |
非碳酸饮料 |
|
平均价格(元 瓶) |
0 |
2 |
3 |
4 |
(3)若我市约有初中生4万人,估计我市初中生每天用于饮品上的花费是多少元?
(4)为了养成良好的生活习惯,班主任决定在自带白开水的5名同学(男生2人,女生3人)中随机抽取2名同学做良好习惯监督员,请用列表法或树状图法求出恰好抽到2名女生的概率.
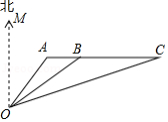
如图,码头 、 分别在海岛 的北偏东 和北偏东 方向上,仓库 在海岛 的北偏东 方向上,码头 、 均在仓库 的正西方向,码头 和仓库 的距离 ,若将一批物资从仓库 用汽车运送到 、 两个码头中的一处,再用货船运送到海岛 ,若汽车的行驶速度为 ,货船航行的速度为 ,问这批物资在哪个码头装船,最早运抵海岛 ?(两个码头物资装船所用的时间相同,参考数据: ,
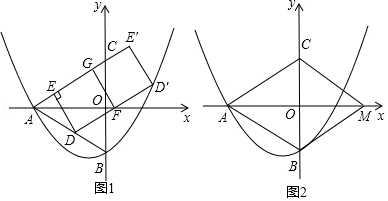
如图1,抛物线 经过 , 、 两点,点 在 轴上, 为等边三角形,点 从点 出发,沿 方向以每秒2个单位长度的速度向终点 运动,设运动时间为 秒 ,过点 作 于点 ,以 为边作矩形 ,使点 在 轴上,点 在 或 的延长线上.
(1)求抛物线的解析式;
(2)将矩形 沿 所在直线翻折,得矩形 ,当点 的对称点 落在抛物线上时,求此时点 的坐标;
(3)如图2,在 轴上有一点 , ,连接 、 ,在点 的运动过程中,设矩形 与四边形 重叠部分的面积为 ,直接写出 与 之间的函数关系式,并写出自变量 的取值范围.
如图1,在 中, , ,点 、 分别在 、 边上, ,连接 、 、 ,点 、 、 分别是 、 、 的中点,连接 、 、 .
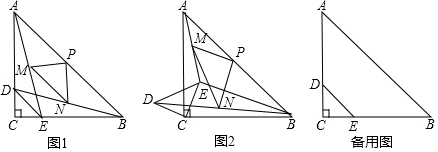
(1) 与 的数量关系是 ;
(2)将 绕点 逆时针旋转到如图2的位置,判断(1)中的结论是否仍然成立,如果成立,请写出证明过程,若不成立,请说明理由;
(3)若 , ,在将图1中的 绕点 逆时针旋转一周的过程中,当 、 、 三点在一条直线上时, 的长度为 .
某超市销售樱桃,已知樱桃的进价为15元 千克,如果售价为20元 千克,那么每天可售出250千克,如果售价为25元 千克,那么每天可获利2000元,经调查发现:每天的销售量 (千克)与售价 (元 千克)之间存在一次函数关系.
(1)求 与 之间的函数关系式;
(2)若樱桃的售价不得高于28元 千克,请问售价定为多少时,该超市每天销售樱桃所获的利润最大?最大利润是多少元?