某校从参加高二年级学业水平测试的学生中抽出80名学生，其数学成绩（均为整数）的频率分布直方图如图所示．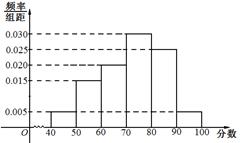
（I）估计这次测试数学成绩的平均分；
（II）假设在[90，100]段的学生的数学成绩都不相同，且都超过94分．若将频率视为概率，现用简单随机抽样的方法，从95，96，97，98，99，100这6个数中任意抽取2个数，有放回地抽取了3次，记这3次抽取中，恰好是两个学生的数学成绩的次数为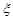
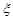，求的分布列及数学期望
．
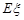已知数列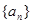
的各项均为正数，
表示该数列前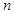
项的和，且满足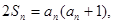
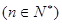，设
（1）求数列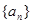的通项；（2）证明：数列
为递增数列；
（3）是否存在正整数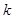
，使得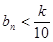
对任意正整数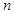恒成立，若存在，求出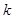的最小值。
已知二次函数
的二次项系数为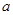
，且不等式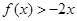
的解集为
。（Ⅰ）若方程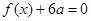
有两个相等的根，求的解析式；
（Ⅱ）若的最大值为正数，求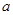的取值范围。
在四棱锥P—ABCD中，底面ABCD是一直角梯形，
，
与底面成30°角。
（1）若
为垂足，求证：
；
（2）在（1）的条件下，求异面直线AE与CD所成角的余弦值；
（3）求平面PAB与平面PCD所成的锐二面角的正切值。
在一次购物抽奖活动中，假设某10张券中有一等奖券1张，可获价值50元的奖品；有二等奖券3张，每张可获价值10元的奖品；其余6张没有奖。某顾客从此10张券中任抽2张，求：
(1) 该顾客中奖的概率；
(2) 该顾客获得的奖品总价值x (元)的概率分布列和期望Ex。
已知函数
（其中
）
（I）求函数
的值域；
（II）若函数
的图象与直线
的两个相邻交点间的距离为
，求函数的单调增区间．