设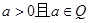 ,
, .
.
(Ⅰ)证明: ;
;
(Ⅱ)求证:在数轴上, 介于
介于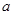 与
与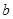 之间,且距
之间,且距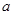 较远;
较远;
(Ⅲ)在数轴上,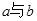 之间的距离是否可能为整数?若有,则求出这个整数;若没有,
之间的距离是否可能为整数?若有,则求出这个整数;若没有,
说明理由.
如图,在平面直角坐标系中,已知平行四边形 的三个顶点坐标:
的三个顶点坐标: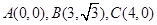 .
.
(1)求边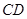 所在直线的方程(结果写成一般式);
所在直线的方程(结果写成一般式);
(2)证明平行四边形 为矩形,并求其面积.
为矩形,并求其面积.
已知函数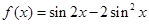
(1)求函数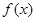 的最小正周期.
的最小正周期.
(2)求函数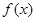 的最大值及
的最大值及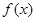 取最大值时x的集合并求函数
取最大值时x的集合并求函数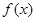 的单调增区间.
的单调增区间.
(本小题满分16分)已知函数 (a为常数).
(a为常数).
(Ⅰ)若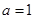 ,写出
,写出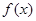 的单调增区间;
的单调增区间;
(Ⅱ)若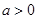 ,设
,设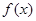 在区间
在区间 上的最小值为
上的最小值为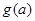 ,求
,求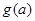 的表达式;
的表达式;
(Ⅲ)设 ,若函数
,若函数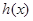 在区间
在区间 上是增函数,求实数a的取值范围.
上是增函数,求实数a的取值范围.
(本小题满分16分)已知函数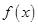 是定义在
是定义在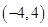 上的奇函数.当
上的奇函数.当 时,
时,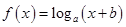 ,且图象过点
,且图象过点 与点
与点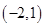 .
.
(Ⅰ)求实数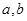 的值,并求函数
的值,并求函数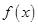 的解析式;
的解析式;
(Ⅱ)若关于 的方程
的方程 有两个不同的实数解,请写出实数
有两个不同的实数解,请写出实数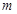 的取值范围;
的取值范围;
(Ⅲ)解关于 的不等式
的不等式 ,写出解集.
,写出解集.
(本小题满分16分)某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品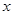 (千台),其总成本为
(千台),其总成本为 (万元),其中固定成本为
(万元),其中固定成本为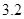 万元,并且每生产1千台的生产成本为
万元,并且每生产1千台的生产成本为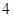 万元(总成本=固定成本+生产成本).销售收入
万元(总成本=固定成本+生产成本).销售收入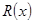 (万元)满足
(万元)满足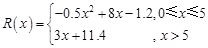 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(Ⅰ)写出利润函数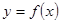 的解析式(利润=销售收入
的解析式(利润=销售收入 总成本);
总成本);
(Ⅱ)工厂生产多少千台产品时,可使盈利最多?