已知椭圆C: 的左、右焦点和短轴的一个端点构成边长为4的正三角形.
的左、右焦点和短轴的一个端点构成边长为4的正三角形.
(1)求椭圆C的方程;
(2)过右焦点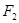 的直线
的直线 与椭圆C相交于A、B两点,若
与椭圆C相交于A、B两点,若 ,求直线
,求直线 的方程.
的方程.
某车队2008年初以98万元购进一辆大客车,并投入营运,第一年需支出各种费用12万元,从第二年起每年支出费用均比上一年增加4万元,该车投入营运后每年的票款收入为50万元,设营运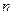 年该车的盈利总额为
年该车的盈利总额为 万元.
万元.
(1)写出 关于
关于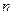 的函数关系式;(2)从哪一年开始,该汽车开始获利;(3)有两种方案处理该车:方案1——当盈利总额达最大值时,年底以20万元的价格卖掉该车;
的函数关系式;(2)从哪一年开始,该汽车开始获利;(3)有两种方案处理该车:方案1——当盈利总额达最大值时,年底以20万元的价格卖掉该车;
方案2——当年均盈利额最大时,年底以40万元的价格卖掉该车.试问车队以哪种方案处理该车获利较大?
已知函数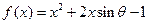
 ,
, (1)当
(1)当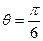 时,求
时,求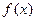 的最大值和最小值(2)若
的最大值和最小值(2)若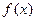 在
在 上是单调增函数,且
上是单调增函数,且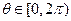 ,求
,求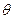 的取值范围.
的取值范围.
已知函数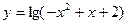 的定义域为A,指数函数
的定义域为A,指数函数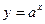 (
(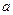 >0且
>0且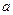 ≠1)(
≠1)(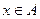 )的值域为B.(1)若
)的值域为B.(1)若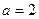 ,求
,求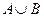 ;(2)若
;(2)若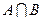 =(
=(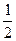 ,2),求
,2),求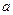 的值.
的值.
.数列 的各项均为正数,
的各项均为正数,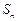 为其前
为其前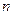 项和,对于任意
项和,对于任意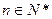 ,总有
,总有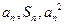 成等差数列.(Ⅰ)求数列
成等差数列.(Ⅰ)求数列 的通项公式;(Ⅱ)设数列
的通项公式;(Ⅱ)设数列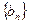 的前
的前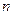 项和为
项和为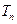 ,且
,且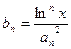 ,求证:对任意实数
,求证:对任意实数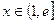 (
(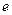 是常数,
是常数,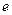 =2.71828
=2.71828 )和任意正整数
)和任意正整数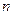 ,总有
,总有
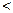 2;(Ⅲ) 正数数列
2;(Ⅲ) 正数数列 中,
中,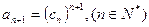 .求数列
.求数列 中的最大项.
中的最大项.
(本小题满分13分)已知点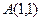 是椭圆
是椭圆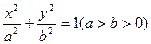 上的一点,
上的一点,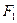 ,
,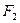 是椭圆的两个焦点,且满足
是椭圆的两个焦点,且满足 .(Ⅰ)求椭圆的方程及离心率;(Ⅱ)设点
.(Ⅰ)求椭圆的方程及离心率;(Ⅱ)设点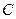 ,
,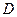 是椭圆上的两点,直线
是椭圆上的两点,直线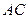 ,
,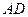 的倾斜角互补,试判断直线
的倾斜角互补,试判断直线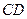 的斜率是否为定值?并说明理由.
的斜率是否为定值?并说明理由.