设无穷数列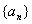 的首项
的首项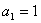 ,前
,前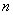 项和为
项和为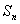 (
(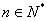 ),且点
),且点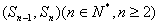 在直线
在直线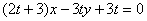 上(
上(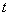 为与
为与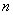 无关的正实数).
无关的正实数).
(1)求证:数列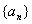 (
(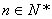 )为等比数列;
)为等比数列;
(2)记数列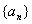 的公比为
的公比为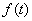 ,数列
,数列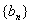 满足
满足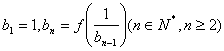 ,设
,设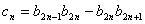 ,求数列
,求数列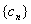 的前
的前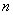 项和
项和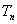 ;
;
(3)若(2)中数列{Cn}的前n项和Tn当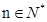 时不等式
时不等式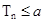 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
已知抛物线C:y=ax2,点P(1,﹣1)在抛物线C上,过点P作斜率为k1、k2的两条直线,分别交抛物线C于异于点P的两点A(x1,y1),B(x2,y2),且满足k1+k2=0.
(1)求抛物线C的焦点坐标;
(2)若点M满足 ,求点M的轨迹方程.
,求点M的轨迹方程.
已知直线l:mx﹣2y+2m=0(m∈R)和椭圆C: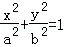 (a>b>0),椭圆C的离心率为
(a>b>0),椭圆C的离心率为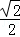 ,连接椭圆的四个顶点形成四边形的面积为2
,连接椭圆的四个顶点形成四边形的面积为2 .
.
(1)求椭圆C的方程;
(2)设直线l经过的定点为Q,过点Q作斜率为k的直线l′与椭圆C有两个不同的交点,求实数k的取值范围;
(3)设直线l与y轴的交点为P,M为椭圆C上的动点,线段PM长度的最大值为f(m),求f(m)的表达式.
已知某椭圆C,它的中心在坐标原点,左焦点为F(﹣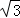 ,0),且过点D(2,0).
,0),且过点D(2,0).
(1)求椭圆C的标准方程;
(2)若已知点A(1, ),当点P在椭圆C上变动时,求出线段PA中点M的轨迹方程.
),当点P在椭圆C上变动时,求出线段PA中点M的轨迹方程.
已知动圆M过定点F(0,﹣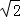 ),且与直线y=
),且与直线y=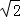 相切,椭圆N的对称轴为坐标轴,一个焦点为F,点A(1,
相切,椭圆N的对称轴为坐标轴,一个焦点为F,点A(1,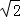 )在椭圆N上.
)在椭圆N上.
(1)求动圆圆心M的轨迹Γ的方程及椭圆N的方程;
(2)若动直线l与轨迹Γ在x=﹣4处的切线平行,且直线l与椭圆N交于B,C两点,试求当△ABC面积取到最大值时直线l的方程.
已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线y2=2px上,△ABC的重心与此抛物线的焦点F重合(如图)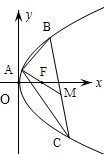
(1)写出该抛物线的方程和焦点F的坐标;
(2)求线段BC中点M的坐标
(3)求BC所在直线的方程.