如图,在C城周边已有两条公路l1,l2在点O处交汇.已知OC=( +
+ )km,∠AOB=75°,∠AOC=45°,现规划在公路l1,l2上分别选择A,B两处为交汇点(异于点O)直接修建一条公路通过C城.设OA=x km,OB=y km.
)km,∠AOB=75°,∠AOC=45°,现规划在公路l1,l2上分别选择A,B两处为交汇点(异于点O)直接修建一条公路通过C城.设OA=x km,OB=y km.
(1)求y关于x的函数关系式并指出它的定义域;
(2)试确定点A,B的位置,使△OAB的面积最小.
(本小题满分12分)
等差数列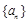 的前n项和为
的前n项和为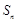 ,数列
,数列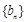 是等比数列,满足
是等比数列,满足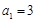 ,
,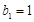 ,
,  ,
,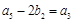 .
.
(Ⅰ)求数列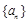 和
和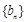 的通项公式;
的通项公式;
(Ⅱ)令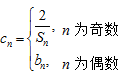 设数列
设数列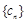 的前n项和
的前n项和 ,求
,求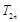 .
.
(本小题满分12分)
四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,且平面SAD⊥平面ABCD,M、N分别是AB、SC的中点.
(Ⅰ)求证:MN∥平面SAD;
(Ⅱ)求二面角S-CM-D的余弦值.
(本小题满分12分)
在科普知识竞赛前的培训活动中,将甲、乙两名学生的6次培训成绩(百分制)制成如图所示的茎叶图:
(Ⅰ)若从甲、乙两名学生中选择1人参加该知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(Ⅱ)若从学生甲的6次培训成绩中随机选择2个,记选到的分数超过87分的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
已知函数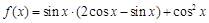 .
.
(Ⅰ)求函数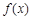 的最小正周期;
的最小正周期;
(Ⅱ)设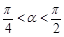 ,且
,且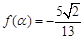 ,求
,求 的值.
的值.
(本题满分18分)本题共3小题,第(1)小题6分,第(2)小题6分,第(3)小题6分.
已知函数 .
. 
(1)指出 的基本性质(结论不要求证明)并作出函数
的基本性质(结论不要求证明)并作出函数 的图像;
的图像;
(2)关于 的不等式
的不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)关于 的方程
的方程 (
( )恰有6个不同的实数解,求
)恰有6个不同的实数解,求 的取值范围.
的取值范围.