如图所示,在△ABC中,I为△ABC的内心,AI交BC于D,交△ABC外接圆于E.
求证:(1)IE=EC;
(2)IE2=ED·EA.
已知函数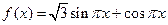 ,
, 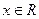 .
.
(1)求函数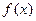 的最大值和最小值;
的最大值和最小值;
(2)设函数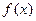 在
在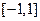 上的图象与
上的图象与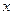 轴的交点从左到右分别为M、N,图象的最高点为P,
轴的交点从左到右分别为M、N,图象的最高点为P,
求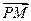 与
与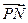 的夹角的余弦.
的夹角的余弦.
(本小题14分)在数列 中,
中,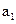 =0,且对任意k
=0,且对任意k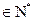 ,
,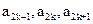 成等差数列,其公差为2k.(Ⅰ)证明
成等差数列,其公差为2k.(Ⅰ)证明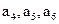 成等比数列;
成等比数列;
(Ⅱ)求数列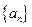 的通项公式;
的通项公式;
(Ⅲ)记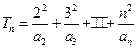 .证明:当
.证明:当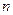 为偶数时, 有
为偶数时, 有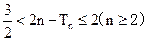 .
.
(本小题14分)已知点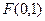 ,直线
,直线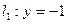 ,
,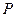 为平面上的动点,过点
为平面上的动点,过点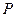 作直线
作直线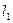 的垂线,垂足为点
的垂线,垂足为点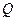 ,且
,且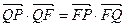 .
.
(1)求动点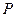 的轨迹
的轨迹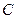 的方程;
的方程;
(2)轨迹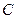 上是否存在一点
上是否存在一点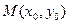 使得过
使得过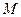 的切线
的切线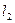 与直线
与直线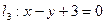 平行?若存在,求出
平行?若存在,求出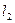 的方程,并求出它与
的方程,并求出它与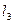 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由.
(14分) 点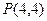 ,圆
,圆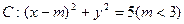 与椭圆
与椭圆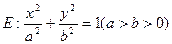 有一个公共点
有一个公共点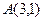 ,
,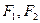 分别是椭圆的左右焦点,直线
分别是椭圆的左右焦点,直线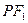 与圆
与圆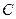 相切.
相切.
(1)求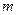 的值;(2)求椭圆
的值;(2)求椭圆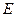 的方程。
的方程。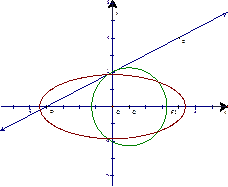
(本小题14分)在等比数列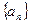 中,
中,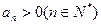 ,公比
,公比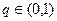 ,且
,且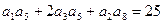 ,又
,又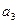 与
与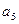 的等比中项是2,
的等比中项是2,
(1)求数列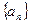 的通项公式;
的通项公式;
(2)设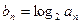 ,数列
,数列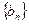 的前
的前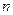 项和为
项和为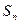 ,求
,求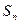 .
.