已知中心在原点的双曲线C的一个焦点是F1(-3,0),一条渐近线的方程是
(1)求双曲线C的方程;
(2)若以k(k≠0)为斜率的直线l与双曲线C相交于两个不同的点M, N,且线段MA的垂直平分线与两坐标轴围成的三角形的面积为 ,求k的取值范围。
,求k的取值范围。
已知{an}是等差数列,其中a2=22,a7=7
(1)求{an}的通项;
(2)求a2+a4+a6+……+a20 的值;
的值;
(3)设数列{an}的前n项和为S n,求S n的最大值
为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计 上午8:00 —10:00间各自的点击量,
上午8:00 —10:00间各自的点击量, 得如下所示的统计图,根据统计图
得如下所示的统计图,根据统计图
| 甲 |
乙 |
||||||
| 8 |
0 |
5 |
6 |
||||
| 1 |
2 |
4 |
9 |
9 |
|||
| 5 |
4 |
0 |
2 |
1 |
|||
| 8 |
3 |
6 |
7 |
||||
| 1 |
4 |
2 |
2 |
5 |
|||
| 8 |
5 |
5 |
4 |
||||
| 7 |
6 |
4 |
6 |
1 |
|||
| 3 |
2 |
0 |
7 |
(1)甲、乙两个网站点击量的极差分别是多少?
(2)甲网站点击量在[10,40]间的频率是多少?
(3)甲、乙两个网站哪个更受欢迎 ?并说明理由。
?并说明理由。
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E为PC的中点,AD=CD=1,DB=2.
(1)证明PA∥平面BDE;
(2)证明AC⊥平面PBD;
(本小题满分14分)
已知函数 .
.
(1)求 的最小正周期;
的最小正周期;
(2)写出函数 的单调递减区间
的单调递减区间
(3)函数 的图象可由
的图象可由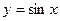 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
(本小题满分12分)
有四个正数,前三个数成等差数列,其和为48,后三个数成等比数列,其最后一个数为函数 的最大值,求这四个数.
的最大值,求这四个数.