如图所示,在矩形ABCD中,AB=a,BC=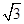 a,以对角线AC为折线将直角三角形ABC向上翻折到三角形APC的位置(B点与P点重合),P点在平面ACD上的射影恰好落在边AD上的H处.
a,以对角线AC为折线将直角三角形ABC向上翻折到三角形APC的位置(B点与P点重合),P点在平面ACD上的射影恰好落在边AD上的H处.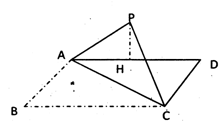
(1)求证:PA⊥CD;
(2)求直线PC与平面ACD所成角的正切值.
已知函数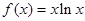 .
.
(1)求曲线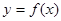 在点(1,0)处的切线方程;
在点(1,0)处的切线方程;
(2)设函数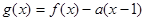 ,其中
,其中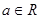 ,求函数
,求函数 在
在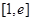 上的最小值.(其中
上的最小值.(其中 为自然对数的底数)
为自然对数的底数)
已知椭圆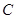 的对称中心为原点
的对称中心为原点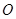 ,焦点在
,焦点在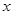 轴上,左右焦点分别为和,且||=2,离心率
轴上,左右焦点分别为和,且||=2,离心率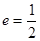 .
.
(1)求椭圆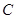 的方程;
的方程;
(2)过的直线与椭圆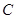 相交于A,B两点,若
相交于A,B两点,若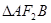 的面积为
的面积为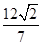 ,求直线
,求直线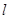 的方程.
的方程.
如图,三棱柱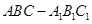 中,侧棱垂直底面,
中,侧棱垂直底面,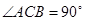 ,
,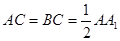 ,
,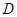 是棱
是棱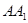 的中点。
的中点。
(1)证明: ⊥平面
⊥平面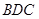
(2)设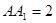 ,求几何体
,求几何体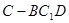 的体积。
的体积。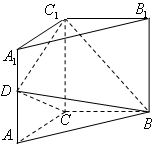
吸烟的危害很多,吸烟产生的烟雾中有近2000种有害物质,如尼古丁、氰氢酸、氨、一氧化碳、二氧化碳、吡啶、砷、铜、铅等,还有40多种致癌物,如苯并芘、朕苯胺及煤焦油等。它们随吸烟者吞咽烟雾时进入体内,对机体产生危害。为了解某市心肺疾病是否与吸烟有关,某医院随机对入院的50人进行了问卷调查,得到了如下的列联表.
| 患心肺疾病 |
不患心肺疾病 |
合计 |
|
| 吸烟患者 |
20 |
5 |
25 |
| 不吸烟患者 |
10 |
15 |
25 |
| 合计 |
30 |
20 |
50 |
(1)用分层抽样的方法在患心肺疾病的人群中抽3人,其中吸烟患者抽到多少人?
(2)在上述抽取的3人中选2人,求恰有一名不吸烟患者的概率;
(3)是否有99.5%的把握认为患心肺疾病与吸烟有关?
附:
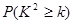 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
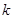 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
参考公式: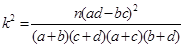 ,其中
,其中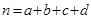
设 的内角
的内角 的对边分别
的对边分别 且
且 ,
, ,若
,若 ,求
,求 的值。
的值。