已知函数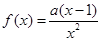 ,其中
,其中 。
。
(1)若直线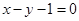 是曲线
是曲线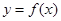 的切线,求a的值;
的切线,求a的值;
(2)设 ,求
,求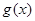 在区间
在区间 上的最大值。(其中e为自然对数的底数)。
上的最大值。(其中e为自然对数的底数)。
有一块边长为4的正方形钢板,现对其切割、焊接成一个长方体无盖容器(切、焊损耗忽略不计)。有人应用数学知识作如下设计:在钢板的四个角处各切去一个全等的小正方形,剩余部分围成一个长方体,该长方体的高是小正方形的边长。
(1)请你求出这种切割、焊接而成的长方体容器的最大容积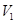 ;
;
(2)请你判断上述方案是否是最佳方案,若不是,请设计一种新方案,使材料浪费最少,且所得长方体容器的容积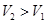 。
。
设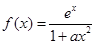 ,其中a为正实数。
,其中a为正实数。
(1)当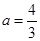 时,求
时,求 的极值点;
的极值点;
(2)若 在R不是单调函数,求a的取值范围。
在R不是单调函数,求a的取值范围。
已知数列 满足
满足 ,且
,且 。
。
(1)求 。
。
(2)猜想数列 的通项公式,并用数学归纳法证明。
的通项公式,并用数学归纳法证明。
(1)证明: ;
;
(2)已知 ,求证:
,求证: 。
。