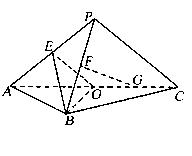
如图,平面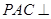 平面
平面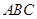 ,
,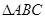 是以
是以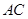 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,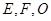 分别为
分别为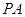 ,
,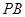 ,
,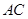 的中点,
的中点,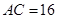 ,
,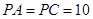 .
.
(1)设 是
是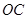 的中点,证明:
的中点,证明: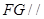 平面
平面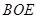 ;
;
(2)证明:在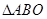 内存在一点
内存在一点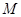 ,使
,使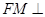 平面
平面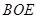 ,并求点
,并求点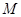 到
到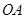 ,
,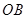 的距离.
的距离.
6本不同的书,按以下要求各有多少种分法?
(1)平均分成三组;
(2)分成1本,2本、3本三组;
(3)平均分给甲、乙、丙三人;
(4)分给甲、乙、丙三人,一人拿1本,一人拿2本、一人拿3本;
(5)甲得一本,乙得二本,丙得三本.
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.
(1)求证:AA1⊥平面ABC;
(2)求二面角A1-BC1-B1的余弦值;
(3)证明:在线段BC1存在点D,使得AD⊥A1B,并求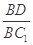 的值.
的值.
如图,四棱锥 的底面
的底面 为菱形,
为菱形, ,侧面
,侧面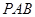 是边长为2的正三角形,侧面
是边长为2的正三角形,侧面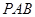
 底面
底面 .
.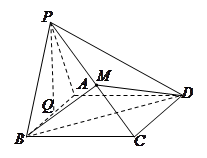
(Ⅰ)设 的中点为
的中点为 ,求证:
,求证: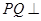 平面
平面 ;
;
(Ⅱ)求斜线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在侧棱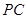 上存在一点
上存在一点 ,使得二面角
,使得二面角 的大小为
的大小为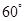 ,求
,求 的值.
的值.
已知正方体ABCD- 的棱长为1,求直线
的棱长为1,求直线 与AC的距离.
与AC的距离.
(高考真题)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(1)求证:AA1⊥平面ABC;
(2)求二面角A1-BC1-B1的余弦值;
(3)证明:在线段BC1上存在点D,使得AD⊥A1B,并求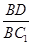 的值.
的值.