已知向量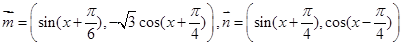 ,函数
,函数

(1)求函数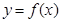 图像的对称中心坐标;
图像的对称中心坐标;
(2)将函数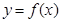 的图像向下平移
的图像向下平移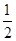 ,再向左平移
,再向左平移 个单位得到函数
个单位得到函数 的图像,是写出
的图像,是写出 的解析式并作出它在
的解析式并作出它在 上的图像。
上的图像。
四棱柱ABCD-A1B1C1D1的三视图和直观图如下.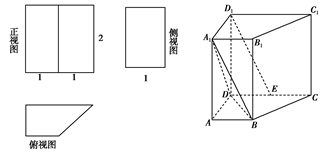
(1)求出该四棱柱的表面积;
(2)设E是DC上一点,试确定E的位置,使D1E∥平面A1BD,并说明理由.
一个正方体的平面展开图及该正方体的直观图的示意图如图所示.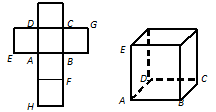
(1)请把字母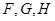 标记在正方体相应的顶点处(不需要说明理由)
标记在正方体相应的顶点处(不需要说明理由)
(2)判断平面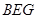 与平面
与平面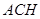 的位置关系.并证明你的结论.
的位置关系.并证明你的结论.
(3)证明:直线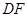
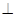 平面
平面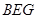
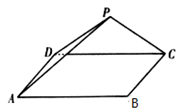
如图,三角形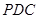 所在的平面与长方形
所在的平面与长方形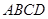 所在的平面垂直,
所在的平面垂直,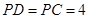 ,
,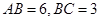 .
.
(1)证明: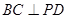 ;
;
(2)求点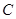 到平面
到平面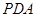 的距离.
的距离.
在正方体ABCD-A1B1C1D1中,E是CD的中点,连接AE并延长与BC的延长线交于点F,连接BE并延长交AD的延长线于点G,连接FG.
求证:直线FG⊂平面ABCD且直线FG∥直线A1B1.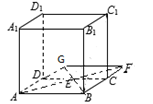
如图,在三棱锥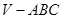 中,平面
中,平面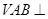 平面
平面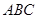 ,
,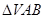 为等边三角形,
为等边三角形, 且
且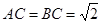 ,
,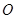 ,
,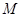 分别为
分别为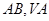 的中点.
的中点.
(1)求证: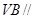 平面
平面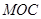 ;
;
(2)求三棱锥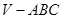 的体积.
的体积.