2014年索契冬季奥运会，已经在2014年02月07日至02月23日在俄罗斯联邦索契市举行.该市为了缓解交通压力，大力发展公共交通.为了调查市民乘公交车的候车情况，交通主管部门从在某站台等车的45名候车乘客中随机抽取15人，按照他们的候车时间（单位：分钟）作为样本分成6组，如下表所示：
（1）估计这45名乘客中候车时间少于12分钟的人数；
（2）若从上表第四、五组的5人中随机抽取2人做进一步的问卷调查，求抽到的2人恰好来自不同组的概率.
如图所示,四棱锥E
ABCD中,EA=EB,AB∥CD,AB⊥BC,AB=2CD.
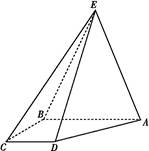
(1)求证:AB⊥ED;
(2)线段EA上是否存在点F,使DF∥平面BCE?若存在,求出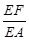
;若不存在,说明理由.
如图五面体中,四边形ABCD是矩形,DA⊥平面ABEF,AB∥EF,AB=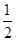
EF=2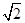
,AF=BE=2,P、Q、M分别为AE、BD、EF的中点.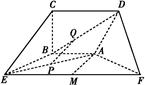
(1)求证:PQ∥平面BCE;
(2)求证:AM⊥平面ADF.
如图,四棱锥S
ABCD的底面是正方形,每条侧棱的长都是底面边长的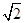
倍,P为侧棱SD上的点.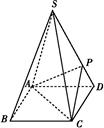
(1)求证:AC⊥SD;
(2)若SD⊥平面PAC,求二面角PACD的大小;
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求SE∶EC的值;若不存在,试说明理由.
如图,在四面体PABC中,PC⊥AB,PA⊥BC,点D,E,F,G分别是棱AP,AC,BC,PB的中点.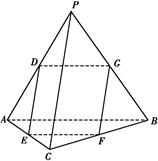
(1)求证:DE∥平面BCP.
(2)求证:四边形DEFG为矩形.
(3)是否存在点Q,到四面体PABC六条棱的中点的距离相等?说明理由.
如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°,E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCD,F为线段A′C的中点.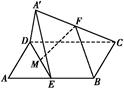
(1)求证:BF∥平面A′DE;
(2)设M为线段DE的中点,求直线FM与平面A′DE所成角的余弦值.