已知椭圆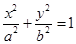 (a>b>0)经过点M(
(a>b>0)经过点M(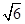 ,1),离心率为
,1),离心率为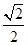 .
.
(1)求椭圆的标准方程;
(2)已知点P(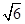 ,0),若A,B为已知椭圆上两动点,且满足
,0),若A,B为已知椭圆上两动点,且满足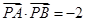 ,试问直线AB是否恒过定点,若恒过定点,请给出证明,并求出该定点的坐标;若不过,请说明理由.
,试问直线AB是否恒过定点,若恒过定点,请给出证明,并求出该定点的坐标;若不过,请说明理由.
(本小题满分14分)
已知函数
(Ⅰ)求f(x)在[-1,e](e为自然对数的底数)上的最 大值;
大值;
(Ⅱ)对任意给定的正实数a,曲线y= f(x)上是否存在两点P,Q,使得△POQ是以O为直角顶点的直角三角形,且此三角形斜边中点在y轴上?
(本小题满分12分)
已知椭圆 的离心率为e=
的离心率为e= ,且过点(
,且过点(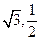 )
)
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线l:y=kx+m(k≠0,m>0)与椭圆交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求:△OPQ面积的最大值及此时直线l的方程.
(本小题满分12分)
某企业科研课题组计划投资研发一种新产品,根据分析和预测,能获得10万元~1000万元的投资收益.企业拟制定方案对课题组进行奖励,奖励方案为:奖金y(单位:万元)随投资收益x(单位:万元)的增加而增加,且奖金不超过9万元,同时奖金也不超过投资收益的20%,并用函数y= f(x)模拟这一奖励方案.
(Ⅰ)试写出模拟函数y= f(x)所满足的条件;
(Ⅱ)试分析函数模型y= 4lgx-3是否符合奖励方案的要求?并说明你的理由.
(本小题满分12分)
已知数列{an}和{bn}满足: a1= ,an+1=
,an+1= an+n-4,bn=(-1)n(an-3n+21),其中
an+n-4,bn=(-1)n(an-3n+21),其中 为实数,n为正整数.
为实数,n为正整数.
(Ⅰ)证明:对 任意实数
任意实数 ,数列{an}不是等比数列;
,数列{an}不是等比数列;
(Ⅱ)证明:当 ≠-18时,数列{bn}是等比数列.
≠-18时,数列{bn}是等比数列.
(本小题满分12分)
如图,平面ABCD⊥平面PAD,△APD是直角三角形,
∠APD=90°,四边形ABCD是直角梯形,其中BC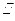 AD,
AD,
∠BAD=90°,AD="2" BC,且AB=BC=PD=2,O是AD的中点,E,F分别是PC,OD的中点.
(Ⅰ)求证:EF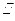 平面PBO;
平面PBO;
(Ⅱ)求二面角A- PF - E的正切值.