用数学归纳法证明:当n是不小于5的自然数时,总有2n>n2成立.
(本小题10分)
某餐厅供应客饭,每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种,现在餐厅准备了五种不同的荤菜,若要保证每位顾客有200种以上不同选择,则餐厅至少还需准备多少不同的素菜品种?(要求写出必要的解答过程)
(本小题满分16分)
已知 ,其中
,其中 是自然常数,
是自然常数,
(1)讨论 时,
时, 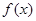 的单调性、极值;
的单调性、极值;
(2)求证:在(1)的条件下, ;
;
(3)是否存在实数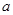 ,使
,使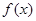 的最小值是3,如果存在,求出
的最小值是3,如果存在,求出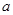 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
(本小题满分16分)
已知数列 中,
中,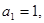 且点
且点 在直线
在直线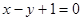 上.
上.
(1)求数列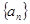 的通项公式;
的通项公式; (2)若函数
(2)若函数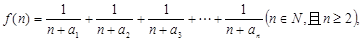 求函数
求函数 的最小值;
的最小值;
(3)设 表示数列
表示数列 的前
的前 项和.试问:是否存在关于
项和.试问:是否存在关于 的整式
的整式 ,使得
,使得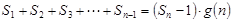 对于一切不小于2的自然数
对于一切不小于2的自然数 恒成立? 若存在,写出
恒成立? 若存在,写出 的解析式,并加以证明;若不存在,试说明理由.
的解析式,并加以证明;若不存在,试说明理由.
(本小题满分16分)
如图,在平面直角坐标系 中,已知点
中,已知点 为椭圆
为椭圆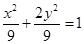 的右顶点, 点
的右顶点, 点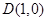 ,点
,点 在椭
在椭
圆上,  .
.
(1)求直线 的方程;
的方程;
(2)求直线 被过
被过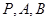 三点的圆
三点的圆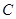 截得的弦长;
截得的弦长;
(3)是否存在分别以 为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不存在,请说明理由.
为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不存在,请说明理由.
(本小题满分14分)
某商店经销一种奥运会纪念品,每件产品的成本为30元,并且每卖出一件产品需向税务部门上交 元(
元( 为常数,2≤a≤5 )的税收.设每件产品的售价为x元(35≤x≤41),根据市场调查,日销售量与
为常数,2≤a≤5 )的税收.设每件产品的售价为x元(35≤x≤41),根据市场调查,日销售量与 (e为自然对数的底数)成反比例.已知每件产品的日售价为40元时,日销售量为10件.
(e为自然对数的底数)成反比例.已知每件产品的日售价为40元时,日销售量为10件.
(1)求该商店的日利润L(x)元与每件产品的日售价x元的函数关系式;
(2)当每件产品的日售价为多少元时,该商品的日利润L(x)最大,并求出L(x)的最大值.