甲、乙两人各掷一次骰子(均匀的正方体,六个面上分别为1,2,3,4,5,6点),所得点数分别为x,y
(1)求x<y的概率;
(2)求5<x+y<10的概率。
如图,设AB,CD为⊙O的两直径,过B作PB垂直于AB,并与CD延长线相交于点P,过P作直线与⊙O分别交于E,F两点,连结AE,AF分别与CD交于G、H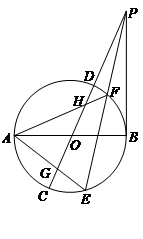
(Ⅰ)设EF中点为 ,求证:O、
,求证:O、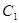 、B、P四点共圆
、B、P四点共圆
(Ⅱ)求证:OG =OH.
已知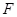 为抛物线
为抛物线 的焦点,抛物线上点
的焦点,抛物线上点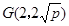 满足
满足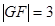
(Ⅰ)求抛物线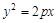 的方程;
的方程;
(Ⅱ)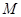 点的坐标为(
点的坐标为(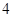 ,
, ),过点F作斜率为
),过点F作斜率为 的直线与抛物线交于
的直线与抛物线交于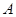 、
、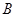 两点,
两点,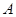 、
、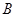 两点的横坐标均不为
两点的横坐标均不为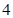 ,连结
,连结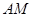 、
、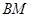 并延长交抛物线于
并延长交抛物线于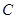 、
、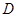 两点,设直线
两点,设直线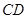 的斜率为
的斜率为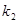 ,问
,问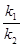 是否为定值,若是求出该定值,若不是说明理由.
是否为定值,若是求出该定值,若不是说明理由.
如图,已知三棱锥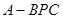 中,
中,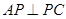 ,
,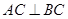 ,
,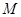 为
为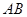 中点,
中点,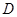 为
为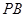 中点,且
中点,且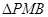 为正三角形。
为正三角形。
(Ⅰ)求证: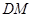 //平面
//平面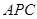 ;
;
(Ⅱ)求证:平面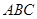 ⊥平面
⊥平面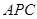 ;
;
(III)若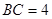 ,
,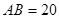 ,求三棱锥
,求三棱锥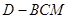 的体积.
的体积.
已知某校在一次考试中,5名学生的数学和物理成绩如下表:
| 学生的编号i |
1 |
2 |
3 |
4 |
5 |
| 数学成绩x |
80 |
75 |
70 |
65 |
60 |
| 物理成绩y |
70 |
66 |
68 |
64 |
62 |
(Ⅰ)若在本次考试中,规定数学成绩在70以上(包括70分)且物理成绩在65分以上(包括65分)的为优秀. 计算这五名同学的优秀率;
(Ⅱ)根据上表,利用最小二乘法,求出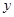 关于
关于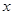 的线性回归方程
的线性回归方程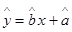 ,其中
,其中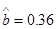
(III)利用(Ⅱ)中的线性回归方程,试估计数学90分的同学的物理成绩.
(四舍五入到整数)
设
(Ⅰ)求函数 的定义域;
的定义域;
(Ⅱ)若存在实数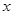 满足
满足 ,试求实数
,试求实数 的取值范围.
的取值范围.