等比数列{an}的各项均为正数，且2a1＋3a2＝1，a＝9a2a6.
(1)求数列{an}的通项公式；
(2)设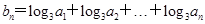
，求数列的前n项和．
设函数f(x)=|2x-1|+|2x-3|,x∈R
(Ⅰ)解不等式f(x)≤5；
(Ⅱ)若
的定义域为R，求实数m的取值范围.
已知曲线C的极坐标方程为
，直线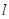
的参数方程为
( t为参数，0≤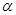
＜
).
(Ⅰ)把曲线C的极坐标方程化为直角坐标方程，并说明曲线C的形状；
(Ⅱ)若直线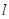经过点(1,0)，求直线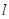被曲线C截得的线段AB的长.
已知函数f（x）=
，x∈[1，3]，
（1）求f（x）的最大值与最小值；
（2）若
于任意的x∈[1，3]，t∈[0，2]恒成立，求实数a的取值范围．
已知两点
及
，点
在以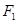
、
为焦点的椭圆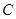
上，且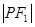
、
、
构成等差数列．
(Ⅰ)求椭圆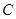的方程；
(Ⅱ)如图，动直线
与椭圆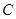有且仅有一个公共点，点
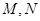是直线
上的两点，且
，
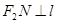． 求四边形
面积
的最大值．
