在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(Ⅰ)求取出的两个球上标号为相同数字的概率;
(Ⅱ)求取出的两个球上标号之积能被3整除的概率.
某校从参加高一年级期末考试的学生中抽出60名学生,将其物理成绩(均为整数)分成六段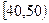 ,
,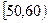 …
…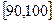 后画出如下频率
后画出如下频率 分布直方图.观察图形的信息,回答下列问题:
分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)估计这次考试的众数m与中位数n(结果保留一位小数);
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和平均分.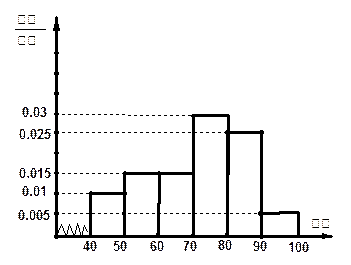
设数列
 。
。
(I) 把算法流程图补充完整:
①处的语句应为;
②处的语句应为;
(Ⅱ) 虚框内的逻辑结构为;
(Ⅲ) 根据流程图写出程序:
分别写出下列命题的逆命题,否命题,逆否命题,并判断其真假.
(1)矩形的对角线相等且互相平分;
(2)正偶数不是质数.
已知函数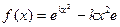 (
(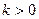 )(
)(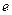 为自然对数的底数)
为自然对数的底数)
(1)求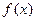 的极值
的极值
(2)对于数列 ,
,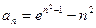 (
(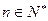 )
)
①证明:
②考察关于正整数
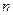 的方程
的方程 是否有解,并说明理由
是否有解,并说明理由