已知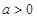 ,函数
,函数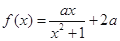 ,
,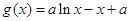 .
.
(1)求函数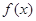 的单调区间;
的单调区间;
(2)求证:对于任意的 ,都有
,都有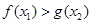 .
.
已知函数
(1)试求b,c所满足的关系式;
(2)若b=0,方程 有唯一解,求a的取值范围.
有唯一解,求a的取值范围.
某公司春节联欢会预设一抽奖活动:在一个不透明的口袋中装入外形一样,号码分别为1,2,3,…,10的十个小球。活动者一次从中摸出三个小球,三球号码有且仅有两个连号的为三等奖,奖金30元;三球号码都连号为二等奖,奖金60元;三球号码分别为1,5,10为一等奖,奖金240元;其余情况无奖金。
(1)员工甲抽奖一次所得奖金的分布列与期望;
(2)员工乙幸运地先后获得四次抽奖机会,他得奖次数的方差是多少?
某学校课题组为了研究学生的数学成绩和物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩,列出如下所示2×2列联表:
| 数学成绩 物理成绩 |
优秀 |
不优秀 |
合计 |
| 优秀 |
5 |
2 |
7 |
| 不优秀 |
1 |
12 |
13 |
| 合计 |
6 |
14 |
20 |
(1)根据题中表格的数据计算,你有多少的把握认为学生的数学成绩与物理成绩之间有关系?
(2)若按下面的方法从这20人(序号1,2,3,…,20)中抽取1人来了解有关情况:将一个标有数字1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号.试求:①抽到12号的概率;②抽到 “无效序号(序号大于20)”的概率.
参考公式: ,其中
,其中 )
)
临界值表供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
已知函数y=f(x)对任意的实数ab都有:f(a+b)=f(a)+f(b)﹣1,且x>0时,f(x)>1,
(1)求证:f(x)是R上的增函数;
(2)若f(4)=5,求f(2)的值,并解不等式f(3m2﹣m﹣2)<3.
已知f(x)=ax3+bx2+cx(a≠0)在x=1和x=-1时取得极值,且f(1)=-1.
(1)试求常数a、b、c的值;
(2)试求f(x) 的单调区间;
(3) 试判断x=±1时函数取极小值还是极大值,并说明理由.