设的内角所对边的长分别是,且
(1)求的值;
(2)求的值.
已知集合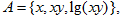 集合
集合 ,若A="B" ,求
,若A="B" ,求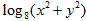 的值.
的值.
(1)已知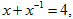 求
求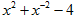 的值;
的值;
(2)已知 ,求
,求 的值.
的值.
计算:
(1) ;
;
(2)2lg5+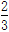 lg8+lg5×lg20+lg22.
lg8+lg5×lg20+lg22.
某单位用2160万元购得一块空地,计划在该空地上建造一栋至少10层,每层2000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).
(1)写出楼房平均综合费用y关于建造层数x的函数关系式;
(2)该楼房应建造多少层时,可使楼房每平方米的平均综合费用最少?最少值是多少?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用=购地总费用/建筑总面积)
已知数列{an}的前n项和为Sn,且向量a=(n,Sn),b=(4,n+3)共线.
(1)求证:数列{an}是等差数列;
(2)求数列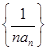 的前n项和Tn.
的前n项和Tn.