(本小题满分12分)某高中为了推进新课程改革,满足不同层次学生的需求,决定从高一年级开始,在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座。(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各学科讲座各天的满座的概率如下表:
根据上表:
(1)求数学辅导讲座在周一、周三、周五都不满座的概率;
(2)设周三各辅导讲座满座的科目数为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
已知tanx=2,则 = .
= .
某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的结果如下:
| 日销售量 |
1 |
1.5 |
2 |
| 频数 |
10 |
25 |
15 |
| 频率 |
0.2 |
a |
b |
(1)求表中a,b的值
(2)若以上表频率作为概率,且每天的销售量相互独立,
①求5天中该种商品恰有2天销售量为1.5吨的概率;
②已知每吨该商品的销售利润为2千元,X表示该种商品两天销售利润的和(单位:千元),求X的分布列和期望.
某班同学利用五一节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念,则称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
| 组数 |
分组 |
低碳族 的人数 |
占本组 的频率 |
| 1 |
[25,30) |
120 |
0.6 |
| 2 |
[30,35) |
195 |
P |
| 3 |
[35,40) |
100 |
0.5 |
| 4 |
[40,45) |
a |
0.4 |
| 5 |
[45,50) |
30 |
0.3 |
| 6 |
[50,55) |
15 |
0.3 |
(1)请补全频率分布直方图,并求n、a、p的值;
(2)在所得样本中,从[40,50)岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动,其中选取3人作为领队,记选取的3名领队中年龄在[40,45)岁的人数为X,求X的分布列和数学期望EX.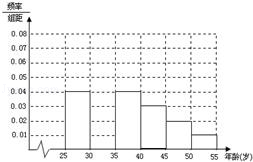
有A、B、C、D、E五位学生的数学成绩x与物理成绩y(单位:分)如下表:
| x |
80 |
75 |
70 |
65 |
60 |
| y |
70 |
66 |
68 |
64 |
62 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程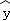 =
=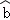 x+
x+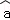 ;
;
(2)若学生F的数学成绩为90分,试根据(1)求出的线性回归方程,预测其物理成绩(保留整数)
(参考数值:80×70+75×66+70×68+65×64+60×62=23190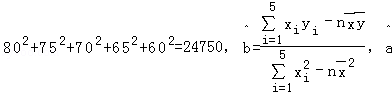 =
=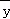
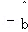
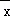 .
.
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| 喜爱打篮球 |
不喜爱打篮球 |
合计 |
|
| 男生 |
5 |
||
| 女生 |
10 |
||
| 合计 |
50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为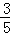 .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
下面的临界值表供参考:
| p(K2≥k) |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: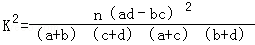 ,其中n=a+b+c+d)
,其中n=a+b+c+d)