在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.圆C1,直线C2的极坐标方程分别为ρ=4sinθ,ρcos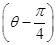 =2
=2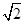 .
.
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点.已知直线PQ的参数方程为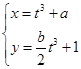 (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.
如图,在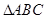 中,
中,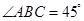 ,
, ,
,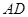 是
是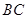 上的高,沿
上的高,沿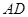 把
把 折起,使
折起,使 .
.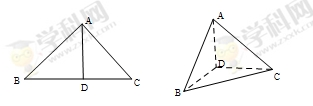
(1)证明:平面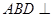 平面
平面 ;
;
(2)设 ,求三棱锥
,求三棱锥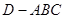 的体积.
的体积.
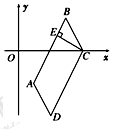
如图,在平行四边形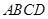 中,边
中,边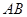 所在的直线方程为
所在的直线方程为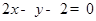 ,点
,点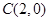 .
.
(1)求直线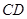 的方程;
的方程;
(2)求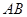 边上的高
边上的高 所在的直线方程.
所在的直线方程.
已知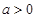 ,函数
,函数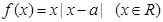 .
.
(1)当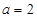 时,画出函数
时,画出函数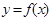 的大致图像;
的大致图像;
(2)当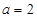 时,根据图像写出函数
时,根据图像写出函数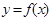 的单调减区间,并用定义证明你的结论;
的单调减区间,并用定义证明你的结论;
(3)试讨论关于x的方程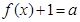 解的个数.
解的个数.
心理学家通过研究学生的学习行为发现;学生的接受能力与老师引入概念和描述问题所用的时间相关,教学开始时,学生的兴趣激增,学生的兴趣保持一段较理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用 表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系:
表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系:

(1)开讲后第5min与开讲后第20min比较,学生的接受能力何时更强一些?
(2)开讲后多少min学生的接受能力最强?能维持多少时间?
(3)若一个新数学概念需要55以上(包括55)的接受能力以及13min时间,那么老师能否在学生一直达到所需接受能力的状态下讲授完这个概念?
已知幂函数 (
(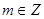 )在
)在 是单调减函数,且为偶函数.
是单调减函数,且为偶函数.
(1)求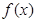 的解析式;
的解析式;
(2)讨论 的奇偶性,并说明理由.
的奇偶性,并说明理由.