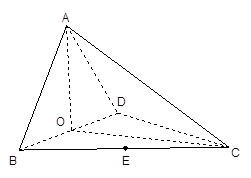某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样,回答问题统计结果如图表所示.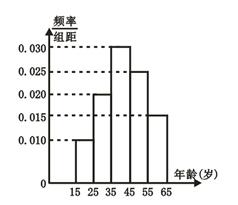
| 组别 |
分组 |
回答正确的人数 |
回答正确的人数占本组的概率 |
| 第1组 |
[15,25) |
5 |
0.5 |
| 第2组 |
[25,35) |
 |
0.9 |
| 第3组 |
[35,45) |
27 |
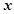 |
| 第4组 |
[45,55) |
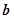 |
0.36 |
| 第5组 |
[55,65) |
3 |
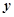 |
(1)分别求出 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
某玩具厂生产一种儿童智力玩具,每个玩具的材料成本为20元,加工费为t元(t为常数,且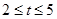 ),出厂价为x元
),出厂价为x元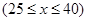 ,根据市场调查知,日销售量q(单位:个)与
,根据市场调查知,日销售量q(单位:个)与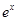 成反比,且当每个玩具的出厂价为30元时,日销售量为100个。
成反比,且当每个玩具的出厂价为30元时,日销售量为100个。
(1)求该玩具厂的日利润y元与每个玩具的出厂价x元之间的函数关系式;
(2)若t=5,则每个玩具的出厂价为x为多少元时,该工厂的日利润y最大?并求最大值。
某高中采取分层抽样的方法从应届高二学生中按照性别抽出20名学生作为样本,其选报文科理科的情况如下表所示.
| 性别 科目 |
男 |
女 |
| 文科 |
2 |
5 |
| 理科 |
10 |
3 |
(Ⅰ)若在该样本中从报考文科的男生和报考理科的女生中随机地选出3人召开座谈会,试求3人中既有男生也有女生的概率;
(Ⅱ)用独立性检验的方法分析有多大的把握认为该中学的高三学生选报文理科与性别有关? (参考公式和数据:χ2 (其中
(其中 ))
))
抛物线 有一内接直角三角形,直角的顶点在原点,一直角边的方程是
有一内接直角三角形,直角的顶点在原点,一直角边的方程是 ,斜边长是
,斜边长是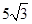 ,求此抛物线的方程。
,求此抛物线的方程。
对某班级50名同学一年来参加社会实践的次数进行的调查统计,得到如下频率分布表:
| 参加次数 |
0 |
1 |
2 |
3 |
| 人数 |
0.1 |
0.2 |
0.4 |
0.3 |
根据上表信息解答以下问题:
(1)从该班级任选两名同学,用η表示这两人参加社会实践次数之和,记“函数 在区间
在区间 ,
,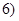 内有零点”的事件为
内有零点”的事件为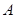 ,求
,求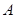 发生的概率
发生的概率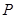 ;
;
(2)从该班级任选两名同学,用ξ表示这两人参加社会实践次数之差的绝对值,求随机变量ξ的分布列及数学期望Eξ
如图,四面体 中,
中,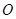 、
、 分别是
分别是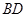 、
、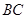 的中点,
的中点,
(1)求证: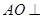 平面
平面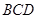 ;
;
(2)求直线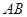 与平面
与平面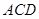 所成角的余弦值;
所成角的余弦值;
(3)求点 到平面
到平面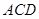 的距离。
的距离。