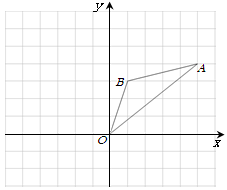
以下是根据北京市统计局公布的2010—2013年北京市城镇居民人均可支配收入和农民人均现金收入的数据绘制的统计图的一部分:
根据以上信息,解答下列问题:
(1)2012年农民人均现金收入比2011年城镇居民人均可支配收入的一半少0.05万元,则2012年农民人
均现金收入是 万元,请根据以上信息补全条形统计图,并标明相应的数据(结果精确到0.1);
(2)在2010—2013年这四年中,北京市城镇居民人均可支配收入和农民人均现金收入相差数额最大的年
份是 年;
(3)①2011—2013年城镇居民人均可支配收入的年平均增长率最接近 ;
| A.14% | B.11% | C.10% | D.9% |
②若2014年城镇居民人均可支配收入按①中的年平均增长率增长,请预测2014年的城镇居民人均可支配收入为 万元(结果精确到0.1).
如图,抛物线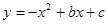 交
交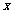 轴于点
轴于点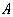 ,交
,交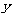 轴于点
轴于点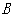 ,已知经过点
,已知经过点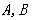 的直线的表达式为
的直线的表达式为 .
.
(1)求抛物线的函数表达式及其顶点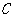 的坐标;
的坐标;
(2)如图①,点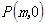 是线段
是线段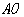 上的一个动点,其中
上的一个动点,其中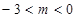 ,作直线
,作直线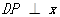 轴,交直线
轴,交直线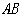 于
于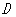 ,交抛物线于
,交抛物线于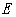 ,作
,作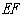 ∥
∥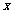 轴,交直线
轴,交直线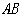 于点
于点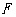 ,四边形
,四边形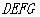 为矩形.设矩形
为矩形.设矩形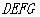 的周长为
的周长为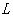 ,写出
,写出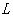 与
与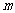 的函数关系式,并求
的函数关系式,并求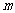 为何值时周长
为何值时周长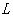 最大;
最大;
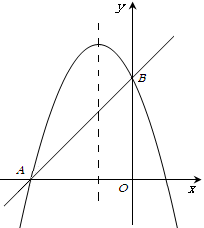
(3)如图②,在抛物线的对称轴上是否存在点 ,使点
,使点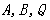 构成的三角形是以
构成的三角形是以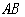 为腰的等腰三角形.若存在,直接写出所有符合条件的点
为腰的等腰三角形.若存在,直接写出所有符合条件的点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.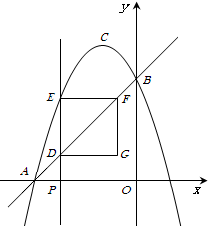
图①图②
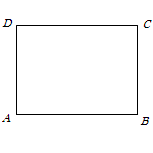
已知,在矩形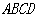 中,连接对角线
中,连接对角线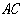 ,将
,将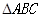 绕点
绕点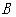 顺时针旋转
顺时针旋转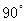 得到
得到 ,并将它沿直线
,并将它沿直线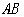 向左平移,直线
向左平移,直线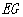 与
与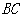 交于点
交于点 ,连接
,连接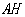 ,
, .
.
(1)如图①,当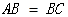 ,点
,点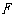 平移到线段
平移到线段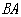 上时,线段
上时,线段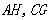 有怎样的数量关系和位置关系?直接写出你的猜想;
有怎样的数量关系和位置关系?直接写出你的猜想;
(2)如图②,当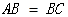 ,点
,点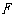 平移到线段
平移到线段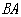 的延长线上时,(1)中的结论是否成立,请说明理由;
的延长线上时,(1)中的结论是否成立,请说明理由;
(3)如图③,当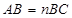
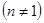 时,对矩形
时,对矩形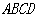 进行如已知同样的变换操作,线段
进行如已知同样的变换操作,线段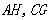 有怎样的数量关系和位置关系?直接写出你的猜想.
有怎样的数量关系和位置关系?直接写出你的猜想.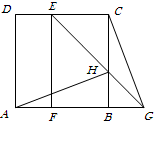
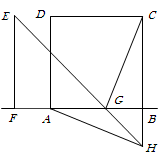
图①图②图③
在“玉龙”自行车队的一次训练中,1号队员以高于其他队员10千米/时的速度独自前行,匀速行进一段时间后,又返回队伍,在往返过程中速度保持不变.设分开后行进的时间为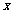 (时),1号队员和其他队员行进的路程分别为
(时),1号队员和其他队员行进的路程分别为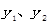 (千米),并且
(千米),并且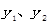 与
与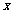 的函数关系如图所示:
的函数关系如图所示: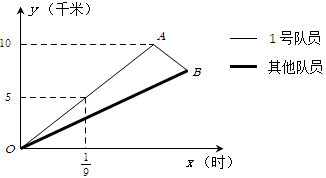
(1)1号队员折返点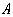 的坐标为,如果1号队员与其他队员经过t小时相遇,那么点
的坐标为,如果1号队员与其他队员经过t小时相遇,那么点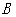 的坐标为;(用含t的代数式表示)
的坐标为;(用含t的代数式表示)
(2)求1号队员与其他队员经过几小时相遇?
(3)在什么时间内,1号队员与其他队员之间的距离大于2千米?
“分组合作学习”成为我市推动课堂教学改革,打造自主高效课堂的重要举措.某中学从全校学生中随机抽取100人作为样本,对“分组合作学习”实施前后学生的学习兴趣变化情况进行调查分析,统计如下:
分组前学生学习兴趣分组后学生学习兴趣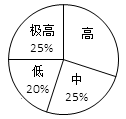
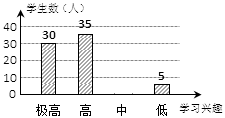
请结合图中信息解答下列问题:
(1)求出分组前学生学习兴趣为“高”的所占的百分比为;
(2)补全分组后学生学习兴趣的统计图;
(3)通过“分组合作学习”前后对比,请你估计全校2000名学生中学习兴趣获得提高的学生有多少人?请根据你的估计情况谈谈对“分组合作学习”这项举措的看法.
如图,在边长为1的正方形组成的网格中, 的顶点均在格点上,其中点
的顶点均在格点上,其中点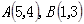 ,将
,将 绕点
绕点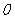 逆时针旋转
逆时针旋转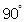 后得到
后得到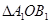 .
.
(1)画出 ;
;
(2)在旋转过程中点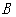 所经过的路径长为;
所经过的路径长为;
(3)求在旋转过程中线段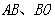 扫过的图形的面积之和.
扫过的图形的面积之和.