在平面直角坐标系中,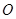 为坐标原点,
为坐标原点,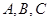 三点满足
三点满足 .
.
(1)求证: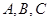 三点共线;
三点共线;
(2)求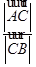 的值;
的值;
(3)已知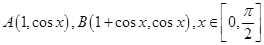 ,
,  的最小值为
的最小值为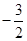 ,求实数
,求实数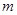 的值.
的值.
设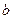 和
和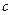 分别是从1,2,3,4这四个数中随机选取的数,用随机变量X表示方程
分别是从1,2,3,4这四个数中随机选取的数,用随机变量X表示方程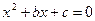 的实根的个数(重根按一个计)。
的实根的个数(重根按一个计)。
(1)求方程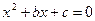 有实根的概率;(2)求随机变量X的分布列和数学期望;
有实根的概率;(2)求随机变量X的分布列和数学期望;
(3)若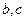 中至少有一个为3,求方程
中至少有一个为3,求方程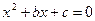 有实根的概率。
有实根的概率。
从一副52张(去掉大小王)的扑克牌中任取一张,求:
(1)这张牌是红桃的概率是多少?
(2)这张牌有人头像(J,Q,K)的概率是多少?
(3)这张牌是红桃的条件下,有人头像的概率是多少
已知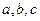 均为实数,且
均为实数,且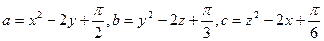 ,求证:
,求证: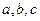 中至少有一个大于
中至少有一个大于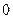 。
。
用数字0、1、2、3、4、5组成没有重复数字
(1)可以组成多少个六位数?
(2)可以组成多少个能被3整除的四位数?
(3)可以组成多少个大于324105的六位数?
一个口袋中有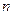 (
(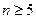 且
且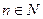 )个红球和5个白球,这些球除颜色外完全相同,每次从袋中任意摸两个球,记录下颜色后,再放回袋中。
)个红球和5个白球,这些球除颜色外完全相同,每次从袋中任意摸两个球,记录下颜色后,再放回袋中。
(1)当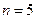 时,设
时,设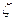 表示第一次摸出的两个球中红球的个数,求
表示第一次摸出的两个球中红球的个数,求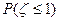
(2)某人共三次摸出球,记三次摸球中恰有一次两球颜色不同的概率为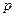 。当
。当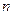 为多少时,
为多少时,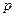 最大?
最大?