设函数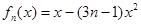 (其中
(其中 ),区间
),区间 .
.
(Ⅰ)定义区间 的长度为
的长度为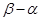 ,求区间
,求区间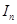 的长度;
的长度;
(Ⅱ)把区间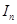 的长度记作数列
的长度记作数列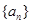 ,令
,令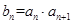 ,
,
(1)求数列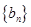 的前
的前 项和
项和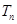 ;
;
(2)是否存在正整数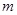 ,
, (
(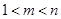 ),使得
),使得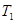 ,
,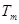 ,
,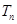 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的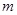 ,
, 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知动圆过定点
, 且在
轴上截得的弦
的长为8.
(Ⅰ) 求动圆圆心的轨迹
的方程;
(Ⅱ) 已知点
, 设不垂直于
轴的直线
与轨迹
交于不同的两点
, 若
轴是
的角平分线, 证明直线
过定点.
在一场娱乐晚会上, 有5位民间歌手(1至5号)登台演唱, 由现场数百名观众投票选出最受欢迎歌手. 各位观众须彼此独立地在选票上选3名选手, 其中观众甲是1号歌手的歌迷, 他必选1号, 不选2号, 另在3至5号中随机选2名. 观众乙和丙对5位歌手的演唱没有偏爱, 因此在1至5号中随机选3名歌手.
(Ⅰ) 求观众甲选中3号歌手且观众乙未选中3号歌手的概率;
(Ⅱ)
表示3号歌手得到观众甲、乙、丙的票数之和, 求
的分布列和数学期望.
如图, 四棱柱
的底面
是正方形,
为底面中心,
平面
,
.
(Ⅰ) 证明:
平面
;
(Ⅱ) 求平面
与平面
的夹角
的大小.
设
是公比为
的等比数列.
(Ⅰ) 推导
的前
项和公式;
(Ⅱ) 设
, 证明数列
不是等比数列.
已知向量
, 设函数
.
(Ⅰ) 求
的最小正周期.
(Ⅱ) 求
在
上的最大值和最小值.