某房地产开发公司用2.56×107元购得一块空地，计划在该空地上建造一栋至少10层，每层2000平方米的楼房，经测算，如果将楼房建为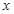
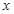（≥10）层，则每平米的平均建筑费用为1000+50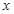（单位：元）
（Ⅰ）写出楼房平均综合费用y关于建造层数x的函数关系式；
（Ⅱ）该楼房应建造多少层时，可使楼房每平米的平均综合费用最少？最少费用是多少？（注：平均综合费用=平均建筑费用+平均购地费用，平均购地费用=
）
已知：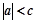
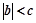，求证：
.
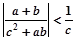已知圆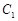
的参数方程为
（
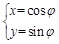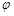为参数），以坐标原点
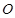为极点，x轴的正半轴为极轴建立极坐标系，圆
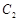的极坐标方程为
．
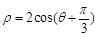（Ⅰ）将圆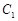的参数方程化为普通方程，将圆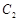的极坐标方程化为直角坐标方程；
（Ⅱ）圆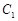、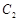是否相交，若相交，请求出公共弦的长；若不相交，请说明理由．
如图，已知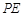
切⊙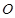
于点E，割线PBA交⊙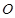于A、B两点，∠APE的平分线和AE、BE分别交于点C、D．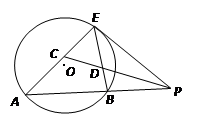
求证：
（Ⅰ）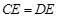
；
（Ⅱ）
．
已知f(x)=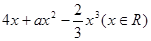
在区间[－1，1]上是增函数.
（Ⅰ）求实数a的值组成的集合A；
（Ⅱ）设关于x的方程f(x)=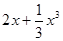
的两个非零实根为x1、x2.试问：是否存在实数m，使得不等式m2+tm+1≥|x1－x2|对任意a∈A及t∈[－1，1]恒成立？若存在，求m的取值范围；若不存在，请说明理由.
曲线C上任一点到定点(0，
)的距离等于它到定直线
的距离.
(1)求曲线C的方程；
(2)经过P(1,2)作两条不与坐标轴垂直的直线
分别交曲线C于A、B两点，且
⊥，设M是AB中点，问是否存在一定点和一定直线，使得M到这个定点的距离与它到定直线的距离相等.若存在，求出这个定点坐标和这条定直线的方程.若不存在，说明理由.