从一批草莓中,随机抽取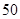 个,其重量(单位:克)的频数分布表如下:
个,其重量(单位:克)的频数分布表如下:
| 分组(重量) |
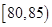 |
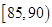 |
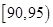 |
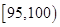 |
| 频数(个) |
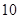 |
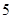 |
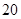 |
 |
(Ⅰ)根据频数分布表计算草莓的重量在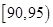 的频率;
的频率;
(Ⅱ)用分层抽样的方法从重量在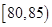 和
和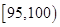 的草莓中共抽取
的草莓中共抽取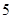 个,其中重量在
个,其中重量在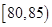 的有几个?
的有几个?
(Ⅲ)在(Ⅱ)中抽出的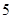 个草莓中,任取
个草莓中,任取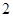 个,求重量在
个,求重量在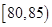 和
和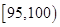 中各有
中各有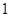 个的概率.
个的概率.
(本题满分12分,第1小题6分,第小题6分)
设函数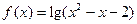 的定义域为集合A,函数
的定义域为集合A,函数 的定义域为集合B。
的定义域为集合B。
(1)求A∩B;
(2)若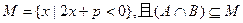 ,求实数
,求实数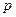 的取值范围。
的取值范围。
(本小题满分14分)已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点。
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线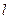 ,使得直线
,使得直线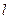 与椭圆C有公共点,且直线OA与
与椭圆C有公共点,且直线OA与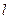 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线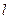 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
(本小题满分14分)已知 c>0, 设命题p:指数函数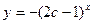 在实数集R上为增函数,命题q:不等式
在实数集R上为增函数,命题q:不等式 在R上恒成立.若命题p或q是真命题, p且q是假命题,求c的取值范围.
在R上恒成立.若命题p或q是真命题, p且q是假命题,求c的取值范围.
某种产品的广告费支出 (单位:百万元)与销售额
(单位:百万元)与销售额 (单位:百万元)之间有如下对应数据
(单位:百万元)之间有如下对应数据
 |
2 |
4 |
5 |
6 |
8 |
 |
30 |
40 |
60 |
50 |
70 |
(1)画出散点图;
(2)求线性回归方程;
(公式: )
)
(3)预测当广告费支出为7百万元时的销售额。
(本小题满分13分)某商场举行抽奖活动,从装有编号0,1,2,3四个球的抽奖箱中,每次取出后放回,连续取两次,取出的两个小球号码相加之和等于5中一等奖,等于4中二等奖,等于3中三等奖。
(1)求中二等奖的概率;
(2)求未中奖的概率。