已知函数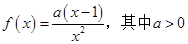 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若直线 是曲线
是曲线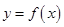 的切线,求实数
的切线,求实数 的值;
的值;
(3)设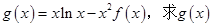 在区间
在区间 上的最小值.(其中e为自然对数的底数)
上的最小值.(其中e为自然对数的底数)
设函数 的图象如图所示,且与
的图象如图所示,且与 在原点相切,若函数的极小值为
在原点相切,若函数的极小值为 ,(1)求
,(1)求 的值;(2)求函数的递减区间.
的值;(2)求函数的递减区间.
如图,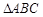 的角平分线
的角平分线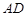 的延长线交它的外接圆于点
的延长线交它的外接圆于点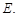
(Ⅰ)证明: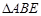 ∽△
∽△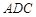 ;
;
(Ⅱ)若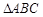 的面积
的面积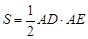 ,求
,求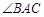 的大小.
的大小.
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出500件,量其内径尺寸,的结果如下表:
甲厂:
乙厂:
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由以上统计数据填下面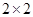 列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”.
| 甲 厂 |
乙 厂 |
合计 |
|
| 优质品 |
|||
| 非优质品 |
|||
| 合计 |
附: 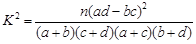
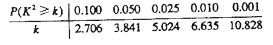
已知三角形ABC的三边长为a、b、c,且其中任意两边长均不相等.若 ,
, ,
, 成等差数列.(1)比较
成等差数列.(1)比较 与
与 的大小,并证明你的结论;(2)求证B不可能是钝角
的大小,并证明你的结论;(2)求证B不可能是钝角
通过市场调查,得到某产品的资金投入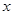 (万元)与获得的利润
(万元)与获得的利润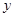 (万元)的数据,如下表所示:
(万元)的数据,如下表所示:
(1)根据上表提供的数据,用最小二乘法求线性回归直线方程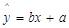 ;
;
(2)现投入资金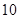 (万元),求估计获得的利润为多少万元.
(万元),求估计获得的利润为多少万元.
资金入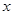 |
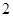 |
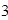 |
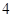 |
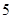 |
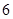 |
利润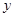 |
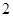 |
3 |
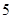 |
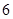 |
 |