已知函数f（x）＝x3＋ax2－a2x＋2，a∈R.
（1）若a＜0时，试求函数y＝f（x）的单调递减区间；
（2）若a＝0，且曲线y＝f（x）在点A、B（A、B不重合）处切线的交点位于直线x＝2上，证明：A、B两点的横坐标之和小于4；
（3）如果对于一切x1、x2、x3∈[0,1]，总存在以f（x1）、f（x2）、f（x3）为三边长的三角形试求正实数a的取值范围．
如图所示，在三棱锥A—BCD中，侧面ABD、ACD是全等的直角三角形，AD是公共的斜边，且AD＝
，BD＝CD＝1，另一个侧面ABC是正三角形.
(1)当正视图方向与向量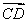
的方向相同时，画出三棱锥A—BCD的三视图;(要求标出尺寸)
(2)求二面角B—AC—D的余弦值;
(3)在线段AC上是否存在一点E，使ED与平面BCD成30°角？ 若存在，确定点E的位置；若不存在，说明理由.
如图,在斜三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成60°的 角,AA1=2.底面ABC是边长为2的正三角形,其重心为G点,E是线段BC1上一点,且BE=3BC1.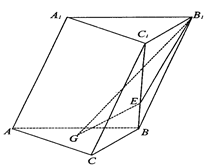
(1)求证:GE∥侧面AA1B1B;
(2)求平面B1GE与底面ABC所成锐二面角的正切值;
(3)求点B到平面B1GE的距离.
如图，直四棱柱ABCD－A1B1C1D1的底面ABCD为平行四边形，其中AB＝
， BD＝BC＝1， AA1＝2，E为DC的中点，F是棱DD1上的动点．
(1)求异面直线AD1与BE所成角的正切值；
(2)当DF为何值时，EF与BC1所成的角为90°？
如图，四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA＝AB＝2PD.
(1)证明：平面PQC⊥平面DCQ；
(2)求二面角D—PQ—C的余弦值.
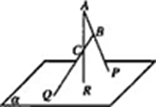
(1)如图,ABC在平面外,AB∩=P,BC∩=Q,AC∩=R,求证:P,Q,R三点共线.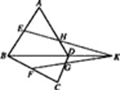
(2)如图,空间四边形ABCD中,E,F分别是AB和CB上的点,G,H分别是CD和AD上的点,且EH与FG相交于点K. 求证:EH,BD,FG三条直线相交于同一点.