已知空间直角坐标系O﹣xyz中的点A(1,1,1),平面α过点A且与直线OA垂直,动点P(x,y,z)是平面α内的任一点.
(1)求点P的坐标满足的条件;
(2)求平面α与坐标平面围成的几何体的体积.
设函数 .
(1)若
的两个极值点为
,且
,求实数
的值;
(2)是否存在实数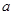 ,使得
是
上的单调函数?若存在,求出
的值;若不存在,说明理由.
,使得
是
上的单调函数?若存在,求出
的值;若不存在,说明理由.
已知函数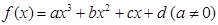 的图象经过原点,
的图象经过原点,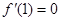 若
若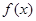 在
在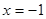 取得极大值2。
取得极大值2。
(1)求函数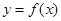 的解析式;
的解析式;
(2)若对任意的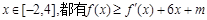 ,求
,求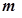 的最大值。
的最大值。
已知10件不同产品中有4件是次品,现对它们进行一一测试,直到选出所有4件次品为止。
(1)若恰在第5次测试,才测试到第一件次品,第十次才找到最后一件次品的不同测试方法数是多少?
(2)若恰在第5次测试后,就找出了所有4件次品,则这样的不同测试方法数是多少?
已知 的展开式中,前三项系数的绝对值依次成等差数列。
的展开式中,前三项系数的绝对值依次成等差数列。
(1)证明:展开式中无常数项;
求展开式中所有有理项。
已知二次函数h(x)=ax2+bx+c(c>0),其导函数y=h′(x)的图象如下,且f(x)=ln x-h(x).
(1)求函数f(x)在x=1处的切线斜率;
(2)若函数f(x)在上是单调函数,求实数m的取值范围;
(3)若函数y=2x-lnx(x∈[1,4])的图象总在函数y=f(x)的图象的上方,求c的取值范围.