(本小题满分14分)在△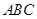 中,内角
中,内角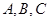 的对边分别为
的对边分别为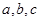 ,已知
,已知
(Ⅰ)求 的值;
的值;
(Ⅱ)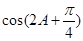 的值.
的值.
【2015高考北京,文19】(本小题满分13分)设函数 ,
, .
.
(Ⅰ)求 的单调区间和极值;
的单调区间和极值;
(Ⅱ)证明:若 存在零点,则
存在零点,则 在区间
在区间 上仅有一个零点.
上仅有一个零点.
【2015高考安徽,文21】已知函数
(Ⅰ)求 的定义域,并讨论
的定义域,并讨论 的单调性;
的单调性;
(Ⅱ)若 ,求
,求 在
在 内的极值.
内的极值.
【2015高考上海,文21】(本小题14分)本题共2小题,第1小题6分,第2小题8分.
如图,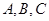 三地有直道相通,
三地有直道相通,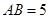 千米,
千米,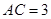 千米,
千米,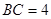 千米.现甲、乙两警员同时从
千米.现甲、乙两警员同时从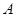 地出发匀速前往
地出发匀速前往 地,经过
地,经过 小时,他们之间的距离为
小时,他们之间的距离为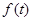 (单位:千米).甲的路线是
(单位:千米).甲的路线是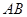 ,速度为5千米/小时,乙的路线是
,速度为5千米/小时,乙的路线是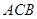 ,速度为8千米/小时.乙到达
,速度为8千米/小时.乙到达 地后原地等待.设
地后原地等待.设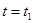 时乙到达
时乙到达 地.
地.
(1)求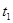 与
与 的值;
的值;
(2)已知警员的对讲机的有效通话距离是3千米.当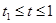 时,求
时,求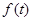 的表达式,并判断
的表达式,并判断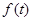 在
在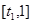 上得最大值是否超过3?说明理由.
上得最大值是否超过3?说明理由.
【2015高考上海,文20】本题共2小题,第1小题6分,第2小题8分.
已知函数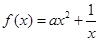 ,其中
,其中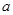 为实数.
为实数.
(1)根据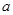 的不同取值,判断函数
的不同取值,判断函数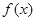 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若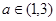 ,判断函数
,判断函数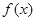 在
在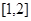 上的单调性,并说明理由.
上的单调性,并说明理由.
【2015高考上海,理20】如图,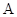 ,
,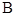 ,
,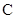 三地有直道相通,
三地有直道相通, 千米,
千米, 千米,
千米, 千米.现甲、乙两警员同时从
千米.现甲、乙两警员同时从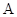 地出发匀速前往
地出发匀速前往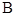 地,经过
地,经过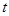 小时,他们之间的距离为
小时,他们之间的距离为 (单位:千米).甲的路线是
(单位:千米).甲的路线是 ,速度为
,速度为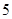 千米/小时,乙的路线是
千米/小时,乙的路线是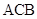 ,速度为
,速度为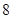 千米/小时.乙到达
千米/小时.乙到达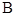 地后原地等待.设
地后原地等待.设 时乙到达
时乙到达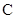 地.
地.
(1)求 与
与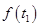 的值;
的值;
(2)已知警员的对讲机的有效通话距离是 千米.当
千米.当 时,求
时,求 的表达式,并判断
的表达式,并判断 在
在 上得最大值是否超过
上得最大值是否超过 ?说明理由.
?说明理由.