已知函数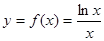 。
。
(Ⅰ)求函数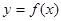 的图像在
的图像在 处的切线方程;
处的切线方程;
(Ⅱ)求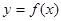 的最大值;
的最大值;
(Ⅲ)设实数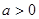 ,求函数
,求函数 在
在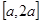 上的最小值
上的最小值
(本小题满分13分) 已知数列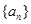 的前
的前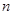 项和是
项和是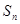 ,且
,且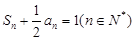 .
.
(1)求数列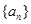 的通项公式;
的通项公式;
(2)设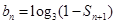 ,求适合方程
,求适合方程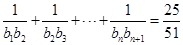 的正整数
的正整数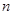 的值.
的值.
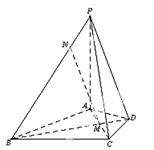
(本小题满分13分)在四棱锥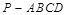 中,
中,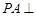 平面
平面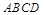 ,
,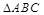 是正三角形,
是正三角形,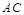 与
与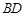 的交点
的交点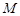 恰好是
恰好是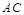 中点,又
中点,又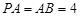 ,
,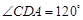 ,点
,点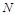 在线段
在线段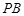 上,且
上,且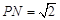 .
.
(1)求证: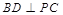 ;
;
(2)求证: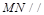 平面
平面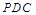 ;
;
(3)求二面角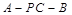 的余弦值.
的余弦值.
(本小题满分13分)已知点 ,
, ,点
,点 为坐标原点,点
为坐标原点,点 在第二象限,且
在第二象限,且 ,记
,记 .
.
(1)求 的值;
的值;
(2)若 ,求
,求 的面积.
的面积.
(本小题满分13分)某小组共有 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2),如下表所示:
五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2),如下表所示:
| A |
B |
C |
D |
E |
|
| 身高 |
1.69 |
1.73 |
1.75 |
1.79 |
1.82 |
| 体重指标 |
19.2 |
25.1 |
18.5 |
23.3 |
20.9 |
(Ⅰ)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率
(Ⅱ)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.
已知椭圆 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,离心率为
轴上,离心率为 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线 的焦点.
的焦点.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)若 ,
, 是椭圆
是椭圆 上关
上关 轴对称的任意两点,设点
轴对称的任意两点,设点 ,连接
,连接 交椭圆
交椭圆 于另一点
于另一点 ,求证:直线
,求证:直线 与
与 轴相交于定点
轴相交于定点 ;
;
(Ⅲ)设 为坐标原点,在(Ⅱ)的条件下,过点
为坐标原点,在(Ⅱ)的条件下,过点 的直线交椭圆
的直线交椭圆 于
于 ,
, 两点,求
两点,求 的取值范围.
的取值范围.