已知二阶矩阵M有特征值λ=8及对应的一个特征向量 =
= ,并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
,并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
(1)求矩阵M;
(2)求矩阵M的另一个特征值,及对应的一个特征向量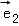 的坐标之间的关系.
的坐标之间的关系.
(3)求直线l:x﹣y+1=0在矩阵M的作用下的直线l′的方程.
已知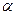 是第一象限的角,且
是第一象限的角,且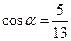 ,求
,求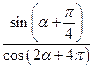 的值。
的值。
将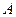 、
、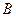 两枚质地均匀骰子各抛掷一次,观察向上的点数,问:
两枚质地均匀骰子各抛掷一次,观察向上的点数,问:
(1)共有多少种不同的结果?
(2)两数之和是3的概率是多少?
(3)两数之和不大于4的概率是多少?
(本小题满分14分)
已知函数
(I)若曲线 与曲线
与曲线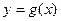 相交,且在
相交,且在 交点处有相同
交点处有相同 的切线,求a的值及该切线的方程;
的切线,求a的值及该切线的方程;
(II)设函数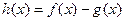 ,当h(x)存在最小值时,求
,当h(x)存在最小值时,求 其最小值
其最小值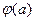 的解析式;
的解析式;
(III)对(II)中的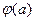 ,证明:当
,证明:当 时,
时,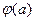

(本小题满分12分)
经市场调查,某种商品在过去50天的销售量和价格均 为销售时间t(天)的函数,且销售量近拟地满足
为销售时间t(天)的函数,且销售量近拟地满足 。前30天价
。前30天价 格为
格为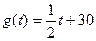
 ,后20天价格为
,后20天价格为
(1)写出该种商品的日销售额S与时间t的函数关系;
(2)求日销售额S的最大值。
(本小题满分12分)
已知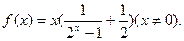
(1 )判断f(x)的奇偶性;
)判断f(x)的奇偶性;
(2)证明