选修4﹣2:矩阵与变换
给定矩阵A=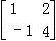 ,B=
,B= .
.
(1)求A的特征值λ1,λ2及对应特征向量α1,α2,
(2)求A4B.
(13分)已知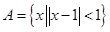 ;
;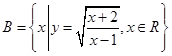 ,求
,求 ,
,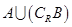 。
。
平面直角坐标系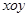 中,直线
中,直线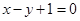 截以原点
截以原点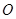 为圆心的圆所得的弦长为
为圆心的圆所得的弦长为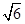
(1)求圆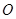 的方程;
的方程;
(2)若直线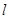 与圆
与圆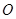 切于第一象限,且与坐标轴交于
切于第一象限,且与坐标轴交于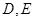 ,当
,当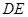 长最小时,求直线
长最小时,求直线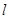 的方程;
的方程;
(3)问是否存在斜率为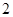 的直线
的直线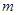 ,使
,使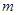 被圆
被圆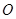 截得的弦为
截得的弦为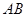 ,以
,以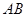 为直径的圆经过原点.若存在,写出直线
为直径的圆经过原点.若存在,写出直线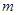 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
如图,三棱柱 中,
中,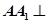 平面
平面 ,
,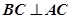 ,
,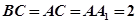 ,
,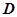 为
为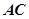 的中点.
的中点.
(1)求证: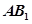 ∥平面
∥平面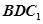 ;
;
(2)求二面角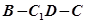 的余弦值;
的余弦值;
(3)设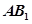 的中点为
的中点为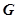 ,问:在矩形
,问:在矩形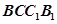 内是否存在点
内是否存在点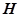 ,使得
,使得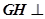 平面
平面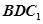 .若存在,求出点
.若存在,求出点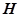 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
已知函数
(1)若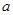 从集合{0,1,2,3}中任取一个元素,
从集合{0,1,2,3}中任取一个元素,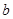 从集合{0,1,2}中任取一个元素,求方程
从集合{0,1,2}中任取一个元素,求方程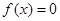 有两个不相等实根的概率;
有两个不相等实根的概率;
(2)若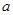 从区间[0,2]中任取一个数,
从区间[0,2]中任取一个数,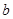 从区间[0,3]中任取一个数,求方程
从区间[0,3]中任取一个数,求方程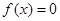 没有实根的概率.
没有实根的概率.
已知函数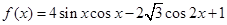 ,且给定条件
,且给定条件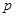 :“
:“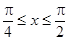 ”。
”。
(1)求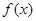 在给定条件
在给定条件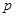 下的最大值及最小值;
下的最大值及最小值;
(2)若又给条件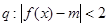 ,且
,且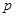 是
是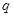 的充分不必要条件,求实数
的充分不必要条件,求实数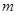 的取值范围。
的取值范围。