设 为奇函数,其图象在点
为奇函数,其图象在点 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数 的最小值为-12.
的最小值为-12.
(1)求 的值;
的值;
(2)求函数 的单调递增区间,极大值和极小值,并求函数f(x)在
的单调递增区间,极大值和极小值,并求函数f(x)在 上的最大值与最小值.
上的最大值与最小值.
已知正项数列{ }的前
}的前 项和为
项和为 ,且
,且 ,
, ,
, 成等差数列.
成等差数列.
(1)证明数列{ }是等比数列;
}是等比数列;
(2)若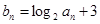 ,求数列
,求数列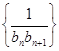 的前
的前 项和
项和 .
.
已知: ,
, 为常数)
为常数)
若 ,求
,求 的最小正周期;
的最小正周期;
若 在
在 上的最大值与最小值之和为3,求
上的最大值与最小值之和为3,求 的值.
的值.
设命题 :函数
:函数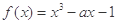 在区间[-1,1]上单调递减;命题
在区间[-1,1]上单调递减;命题 :函数
:函数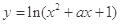 的值域是
的值域是 .如果命题
.如果命题 或
或 为真命题,
为真命题, 且
且 为假命题,求
为假命题,求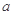 的取值范围.
的取值范围.
已知 ,直线
,直线
(1)函数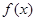 在
在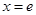 处的切线与直线
处的切线与直线 平行,求实数
平行,求实数 的值
的值
(2)若至少存在一个 使
使 成立,求实数
成立,求实数 的取值范围
的取值范围
(3)设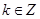 ,当
,当 时
时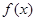 的图像恒在直线
的图像恒在直线 的上方,求
的上方,求 的最大值.
的最大值.