(本小题满分〗2分)
在三棱锥S -ABC中, 是边长为4的正三角形,点S在平面ABC上的射影恰为AC的中点,
是边长为4的正三角形,点S在平面ABC上的射影恰为AC的中点, ,M、N分别为AB、SB的中点.
,M、N分别为AB、SB的中点.
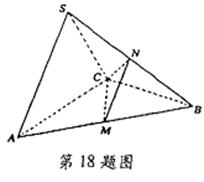
(1) 证明AC丄SB;
(2) 求直线CN与平面ABC所成角的余弦值;
(3) 求点B到平面CMN的距离
(本小题满分12分)
在医学生物学实验中,经常以小老鼠作为实验对象.在甲笼子里关有7只小老鼠(其中5只白色的,2只灰色的),由于都感染了某种烈性病菌,所以想让它们自行分开.以便于进行观察、试验.现有乙笼子是空的,把甲笼子打开一个小孔(只能让小鼠钻出去,再进不来),让小鼠一只一只地往乙笼子跑(假定它们都会争先恐后地从小孔往乙笼跑),直到两只小灰鼠都跑出甲笼子,立即关闭小孔.以f表示甲笼子里还剩下的小白鼠的数目
(1) 求乙笼子里恰好只有2只小灰鼠的概率;
(2) 求 的分布列与数学期望.
的分布列与数学期望.
(本小题满分12分)
巳知函数
(1) 求. 的值域;
的值域;
(2) 求.. .的单调
.的单调 递增区间.
递增区间.
(本小题满分14分)
已知数列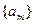 是首项为
是首项为 ,公差为
,公差为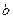 的等差数列,
的等差数列,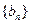 是首项为
是首项为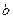 ,公比为
,公比为 的等比数列,且满足
的等比数列,且满足 ,其中
,其中 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若数列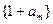 与数列
与数列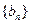 有公共项,将所有公共项按原顺序排列后构成一个新数列
有公共项,将所有公共项按原顺序排列后构成一个新数列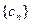 ,求数列
,求数列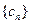 的通项公式;
的通项公式;
(Ⅲ)记(Ⅱ)中数列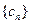 的前项之和为
的前项之和为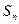 ,求证:
,求证: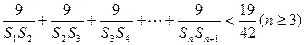 .
.
(本小题满分13分)
已知函数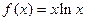
(I)求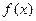 的最小值;
的最小值;
(II)讨论关于x的方程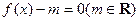 的解的个数;
的解的个数;
(III)当