(本小題满分12分)如图,直角梯形ABCD中,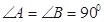 ,AD =" AB" = 2, BC = 3,E,F分别是AD,BC上的两点,且AE=BF=1,G为AB中点,将四边形ABCD沿EF折起到(如图2)所示的位置,使得EG丄GC,连接 AD、BC、AC得(图2)所示六面体.
,AD =" AB" = 2, BC = 3,E,F分别是AD,BC上的两点,且AE=BF=1,G为AB中点,将四边形ABCD沿EF折起到(如图2)所示的位置,使得EG丄GC,连接 AD、BC、AC得(图2)所示六面体.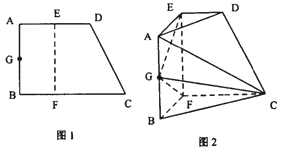
(1)求证:EG丄平面CFG;
(2)求二面角A —CD-E的余弦值.
如图,四边形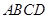 是
是 的内接四边形,
的内接四边形,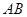 的延长线与
的延长线与 的延长线交于点
的延长线交于点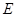 ,且
,且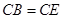 .
.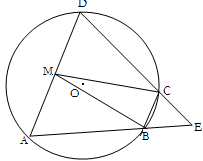
(I)证明: ;
;
(II)设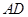 不是
不是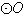 的直径,
的直径,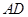 的中点为
的中点为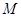 ,且
,且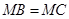 ,证明:
,证明: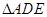 为等边三角形.
为等边三角形.
设函数
,曲线
处的切线斜率为0
求
;若存在
使得
,求
的取值范围。
已知点
,圆
:
,过点
的动直线
与圆
交于
两点,线段
的中点为
,
为坐标原点.
(1)求
的轨迹方程
(2)当
时,求
的方程及
的面积
如图,三棱柱
中,侧面
为菱形,
的中点为
,且
平面
.
(1)证明:
(2)若 , 求三棱柱 的高.
从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量表得如下频数分布表:
| 质量指标值分组 |
[75,85) |
[85,95) |
[95,105) |
[105,115) |
[115,125) |
| 频数 |
6 |
26 |
38 |
22 |
8 |
(I)在答题卡上作出这些数据的频率分布直方图:
(II)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(III)根据以上抽样调查数据,能否认为该企业生产的这种产品符合"质量指标值不低于95的产品至少要占全部产品的80%"的规定?