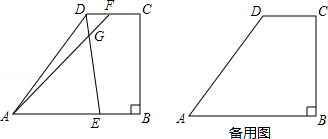
(本题8分)(1)如图1,Rt△ABC中,AB=AC,∠BAC=90°,直线AE是经过点A的任一直线,BD⊥AE于D,CE⊥AE于E,若BD>CE,试问:BD=DE+CE成立吗?请说明理由.
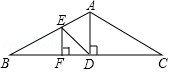
(2)如图2,等腰△ABC中,AB=AC,若顶点A在直线m上,点D、E也在直线m 上,如果∠BAC=∠ADB=∠AEC=1100,那么(1)中结论还成立吗?如果不成立,BD、DE、CE三条线段之间有怎样的关系?并说明理由.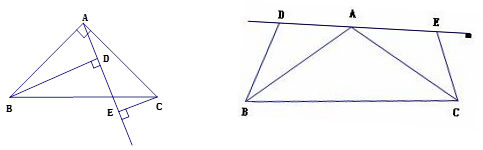
已知在平面直角坐标系 中(如图),已知抛物线 经过点 ,对称轴是直线 ,顶点为 .
(1)求这条抛物线的表达式和点 的坐标;
(2)点 在对称轴上,且位于顶点上方,设它的纵坐标为 ,联结 ,用含 的代数式表示 的余切值;
(3)将该抛物线向上或向下平移,使得新抛物线的顶点 在 轴上.原抛物线上一点 平移后的对应点为点 ,如果 ,求点 的坐标.

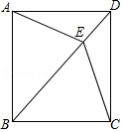
已知:如图,四边形 中, , , 是对角线 上一点,且 .
(1)求证:四边形 是菱形;
(2)如果 ,且 ,求证:四边形 是正方形.
甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
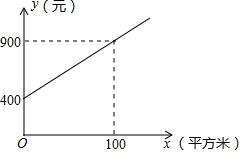
甲公司方案:每月的养护费用 (元 与绿化面积 (平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500 元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.
(1)求如图所示的 与 的函数解析式:(不要求写出定义域);
(2)如果某学校目前的绿化面积是1200平方米,试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.
如图, 一座钢结构桥梁的框架是 ,水平横梁 长 18 米, 中柱 高 6 米, 其中 是 的中点, 且 .
(1) 求 的值;
(2) 现需要加装支架 、 ,其中点 在 上, ,且 ,垂足为点 ,求支架 的长 .
如图所示,梯形 中, , , , , ,点 是边 上的动点,点 是射线 上一点,射线 和射线 交于点 ,且 .
(1)求线段 的长;
(2)如果 是以 为腰的等腰三角形,求线段 的长;
(3)如果点 在边 上(不与点 、 重合),设 , ,求 关于 的函数解析式,并写出 的取值范围.