已知椭圆C的中心在原点,一个焦点为F(0,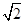 ),且长轴长与短轴长的比是
),且长轴长与短轴长的比是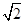 ∶1.
∶1.
(1)求椭圆C的方程;
(2)若椭圆C上在第一象限的一点P的横坐标为1,过点P作倾斜角互补的两条不同的直线PA,PB分别交椭圆C于另外两点A,B,求证:直线AB的斜率为定值.
已知抛物线C:y2=2px(p>0)的焦点为F,抛物线C与直线l1:y=-x的一个交点的横坐标为8.
(1)求抛物线C的方程;
(2)不过原点的直线l2与l1垂直,且与抛物线交于不同的两点A、B,若线段AB的中点为P,且|OP|=|PB|,求△FAB的面积.
已知圆C经过点A(-2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)若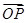 ·
· =-2,求实数k的值.
=-2,求实数k的值.
已知椭圆C: =1(a>b>0)的离心率为
=1(a>b>0)的离心率为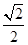 ,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4
,其左、右焦点分别是F1、F2,过点F1的直线l交椭圆C于E、G两点,且△EGF2的周长为4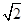 .
.
(1)求椭圆C的方程;
(2)若过点M(2,0)的直线与椭圆C相交于两点A、B,设P为椭圆上一点,且满足 +
+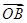 =t
=t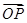 (O为坐标原点),当|
(O为坐标原点),当| -
-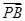 |<
|<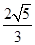 时,求实数t的取值范围.
时,求实数t的取值范围.
已知椭圆E: =1(a>b>0),F1(-c,0),F2(c,0)为椭圆的两个焦点,M为椭圆上任意一点,且|MF1|,|F1F2|,|MF2|构成等差数列,点F2(c,0)到直线l:x=
=1(a>b>0),F1(-c,0),F2(c,0)为椭圆的两个焦点,M为椭圆上任意一点,且|MF1|,|F1F2|,|MF2|构成等差数列,点F2(c,0)到直线l:x= 的距离为3.
的距离为3.
(1)求椭圆E的方程;
(2)若存在以原点为圆心的圆,使该圆的任意一条切线与椭圆E恒有两个交点A,B,且 ⊥
⊥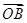 ,求出该圆的方程.
,求出该圆的方程.