本小题满分12分)已知函数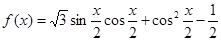 ,
,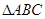 三个内角
三个内角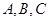 的对边分别为
的对边分别为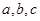 .
.
(Ⅰ)求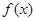 的单调递增区间及对称轴的方程;
的单调递增区间及对称轴的方程;
(Ⅱ)若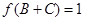 ,
,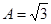
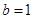 ,求角
,求角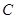 的大小.
的大小.
已知数列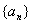 是公差大于
是公差大于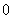 的等差数列,且满足
的等差数列,且满足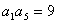 ,
, .
.
(Ⅰ) 求数列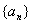 的通项公式;
的通项公式;
(Ⅱ)若数列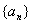 和数列
和数列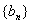 满足等式
满足等式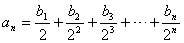 (
( ),求数列
),求数列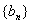 的前
的前 项和
项和 .
.
某学校拟建一块周长为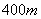 的操场如图所示,操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域,为了能让学生的做操区域尽可能大,试问如何设计矩形的长和宽?(精确到
的操场如图所示,操场的两头是半圆形,中间区域是矩形,学生做操一般安排在矩形区域,为了能让学生的做操区域尽可能大,试问如何设计矩形的长和宽?(精确到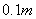 ,取
,取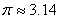 )
)

在 中,
中, 、
、 、
、 所对的边分别是
所对的边分别是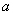 、
、 、
、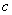 ,其中
,其中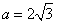 ,
,
 ,求角
,求角 的大小和三角形的面积
的大小和三角形的面积 .
.
(本小题满分14分)已知函数
(1)曲线 经过点P(1,2),且曲线C在点P处的切线平行于直线
经过点P(1,2),且曲线C在点P处的切线平行于直线 ,求a,b的值;
,求a,b的值;
(2)在(1)的条件下试求函数 的极小值;
的极小值;
(3)若 在区间(1,2)内存在两个极值点,求证:
在区间(1,2)内存在两个极值点,求证:
本小题满分14分)已知 中,点A、B的坐标分别为
中,点A、B的坐标分别为 ,点C在x轴上方。
,点C在x轴上方。
(1)若点C坐标为 ,求以A、B为焦点且经过点C的椭圆的方程;
,求以A、B为焦点且经过点C的椭圆的方程;
(2)过点P(m,0)作倾角为 的直线
的直线 交(1)中曲线于M、N两点,若点Q(1,0)恰在以线段MN为直径的圆上,求实数m的值。
交(1)中曲线于M、N两点,若点Q(1,0)恰在以线段MN为直径的圆上,求实数m的值。