(本小题满分12分)如图,已知四棱锥 的底面是菱形,
的底面是菱形, ,
,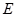 为
为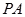 的中点.
的中点.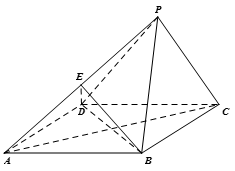
(Ⅰ)求证: ∥平面
∥平面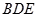 ;
;
(Ⅱ)求证:平面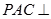 平面
平面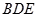 .
.
设数列 的前
的前 项和为
项和为 ,点
,点 在直线
在直线 上.
上.
(1)求数列 的通项公式;
的通项公式;
(2)在 与
与 之间插入
之间插入 个数,使这
个数,使这 个数组成公差为
个数组成公差为 的等差数列,求数列
的等差数列,求数列 的前n项和
的前n项和 .
.
在△ABC中,a,b,c分别为内角A,B,C的对边, 面积
(1)求角C的大小;
(2)设函数 ,求
,求 的最大值,及取得最大值时角B的值.
的最大值,及取得最大值时角B的值.
设命题 “对任意的
“对任意的 ”,命题
”,命题 “存在
“存在 ,使
,使 ”.如果命题
”.如果命题 为真,命题
为真,命题 为假,求实数
为假,求实数 的取值范围.
的取值范围.
已知等比数列{ }的前n项和Sn满足:
}的前n项和Sn满足: ,且
,且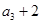 是
是 的等差中项.
的等差中项.
(1)求数列{ }的通项公式;
}的通项公式;
(2)若数列{ }为递增数列,
}为递增数列,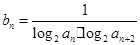 ,
, ,问是否存在最小正整数n使得
,问是否存在最小正整数n使得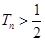 成立?若存在,试确定n的值,不存在说明理由.
成立?若存在,试确定n的值,不存在说明理由.
已知直线 :
: 与圆C:
与圆C: ,
,
(1)若直线 与圆
与圆 相切,求m的值。
相切,求m的值。
(2)若 ,求圆C截直线
,求圆C截直线 所得的弦长。
所得的弦长。