(本题8分)某人去水果批发市场采购苹果,他看中了A、B两家苹果。这两家苹果品质一样,零售价都为6元/千克,批发价各不相同。
A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠。
B家的规定如下表:
| 数量范围(千克) |
0~500 |
500以上~1500 |
1500以上~2500 |
2500以上 |
| 价 格(元) |
零售价的95% |
零售价的85% |
零售价的75% |
零售价的70% |
【表格说明:批发价格分段计算,如:某人批发苹果2100千克,则总费用=6×95%×500+6×85%×1000+6×75%×(2100-1500)】
(1)如果他批发600千克苹果,则他在A 家批发需要 元,在B家批发需要 元;
(2) 如果他批发x千克苹果(1500<x<2000),则他在A 家批发需要 元,在B家批发需要 元(用含x的代数式表示);
(3) 现在他要批发1800千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由。
如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ ABC的三个顶点的坐标分别为 A(﹣1,3), B(﹣4,0), C(0,0)
(1)画出将△ ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△ A 1 B 1 C 1;
(2)画出将△ ABC绕原点 O顺时针方向旋转90°得到△ A 2 B 2 O;
(3)在 x轴上存在一点 P,满足点 P到 A 1与点 A 2距离之和最小,请直接写出 P点的坐标.

若两条抛物线的顶点相同,则称它们为"友好抛物线",抛物线 C 1: y 1=﹣2 x 2+4 x+2与 C 2: y 2=﹣ x 2+ mx+ n为"友好抛物线".
(1)求抛物线 C 2的解析式.
(2)点 A是抛物线 C 2上在第一象限的动点,过 A作 AQ⊥ x轴, Q为垂足,求 AQ+ OQ的最大值.
(3)设抛物线 C 2的顶点为 C,点 B的坐标为(﹣1,4),问在 C 2的对称轴上是否存在点 M,使线段 MB绕点 M逆时针旋转90°得到线段 MB′,且点 B′恰好落在抛物线 C 2上?若存在求出点 M的坐标,不存在说明理由.
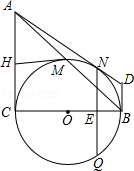
如图,在Rt△ ABC中,∠ C=90°,以 BC为直径的⊙ O交斜边 AB于点 M,若 H是 AC的中点,连接 MH.
(1)求证: MH为⊙ O的切线.
(2)若 ,求⊙ O的半径.
(3)在(2)的条件下分别过点 A、 B作⊙ O的切线,两切线交于点 D, AD与⊙ O相切于 N点,过 N点作 NQ⊥ BC,垂足为 E,且交⊙ O于 Q点,求线段 NQ的长度.
由于持续高温和连日无雨,某水库的蓄水量随时间的增加而减少,已知原有蓄水量 y 1(万 m 3)与干旱持续时间 x(天)的关系如图中线段 l 1所示,针对这种干旱情况,从第20天开始向水库注水,注水量 y 2(万 m 3)与时间 x(天)的关系如图中线段 l 2所示(不考虑其它因素).
(1)求原有蓄水量 y 1(万 m 3)与时间 x(天)的函数关系式,并求当 x=20时的水库总蓄水量.
(2)求当0≤ x≤60时,水库的总蓄水量 y(万 m 3)与时间 x(天)的函数关系式(注明 x的范围),若总蓄水量不多于900万 m 3为严重干旱,直接写出发生严重干旱时 x的范围.

如图, P 1、 P 2是反比例函数 在第一象限图象上的两点,点 A 1的坐标为(4,0).若△ P 1 OA 1与△ P 2 A 1 A 2均为等腰直角三角形,其中点 P 1、 P 2为直角顶点.
(1)求反比例函数的解析式.
(2)①求 P 2的坐标.
②根据图象直接写出在第一象限内当 x满足什么条件时,经过点 P 1、 P 2的一次函数的函数值大于反比例函数 的函数值.
