(本题满分 10分)如图是一个“数值转换机”(箭头是指数进入转换机的路径,方框是对进入的数进行转换的转换机)。
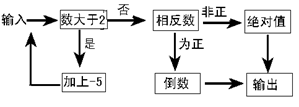
(1)当小明输入4, 7, -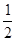 ,-2012 这四个数使,则四次输出的结果依次为 , , , 。
,-2012 这四个数使,则四次输出的结果依次为 , , , 。
(2)你认为当输入数 等于 时(写出一个即可),其输出结果为0。
(3)你认为这个“数值转换机”不可能输出 数。
(4)有一次,小明在操作的时候,输出的结果是2,聪明的你判断一下,小明输入的正整数是 (用含自然数n的代数式表示)。
定义:有三个内角相等的四边形叫三等角四边形.
(1)三等角四边形 中, ,求 的取值范围;
(2)如图,折叠平行四边形纸片 ,使顶点 , 分别落在边 , 上的点 , 处,折痕分别为 , .求证:四边形 是三等角四边形.
(3)三等角四边形 中, ,若 ,则当 的长为何值时, 的长最大,其最大值是多少?并求此时对角线 的长.

为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到 ;活动后,再次检查这部分学生的视力,结果如表所示.
|
分组 |
频数 |
|
|
2 |
|
|
3 |
|
|
5 |
|
|
8 |
|
|
17 |
|
|
5 |
(1)求所抽取的学生人数;
(2)若视力达到4.8及以上为达标,估计活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度分析活动前后相关数据,并评价视力保健活动的效果.

请用学过的方法研究一类新函数 为常数, 的图象和性质.
(1)在给出的平面直角坐标系中画出函数 的图象;
(2)对于函数 ,当自变量 的值增大时,函数值 怎样变化?

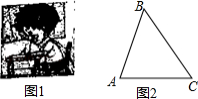
保护视力要求人写字时眼睛和笔端的距离应超过 ,图1是一位同学的坐姿,把他的眼睛 ,肘关节 和笔端 的位置关系抽象成图2的 ,已知 , , ,他的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据: , ,
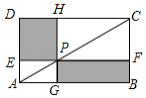
如图,点 在矩形 的对角线 上,且不与点 , 重合,过点 分别作边 , 的平行线,交两组对边于点 , 和 , .
(1)求证: ;
(2)证明四边形 和四边形 都是矩形,并直接写出它们面积之间的关系.