(本小题满分12分)已知双曲线 的离心率为
的离心率为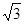 ,点
,点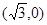 是双曲线的一个顶点.
是双曲线的一个顶点.
(1)求双曲线的方程;
(2)经过的双曲线右焦点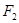 作倾斜角为30°直线
作倾斜角为30°直线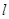 ,直线
,直线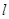 与双曲线交于不同的
与双曲线交于不同的 两点,求
两点,求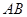 的长.
的长.
已知二次函数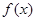 的二次项系数为
的二次项系数为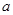 ,且不等式
,且不等式 的解集为(1,3).
的解集为(1,3).
⑴若方程 有两个相等实数根,求
有两个相等实数根,求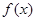 的解析式.
的解析式.
⑵若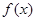 的最大值为正数,求实数
的最大值为正数,求实数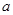 的取值范围.
的取值范围.
已知 、
、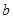 、
、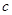 分别是
分别是 的三个内角
的三个内角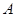 、
、 、
、 的对边.
的对边.
(1)若 面积
面积 求
求 、
、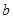 的值;
的值;
(2)若 ,且
,且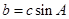 ,试判断
,试判断 的形状.
的形状.
设不等式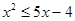 的解集为
的解集为 .
.
(1)求集合 ;
;
(2)设关于 的不等式
的不等式 的解集为
的解集为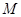 ,若
,若 ,求实数
,求实数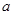 的取值范围.
的取值范围.
设数列{ }是等差数列,数列{
}是等差数列,数列{ }的前
}的前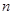 项和
项和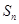 满足
满足 ,
,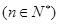 ,且
,且
(1)求数列{ }和{
}和{ }的通项公式:
}的通项公式:
(2)设 为数列{
为数列{ .
. }的前
}的前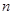 项和,求
项和,求 .
.
火车站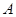 北偏东
北偏东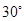 方向的
方向的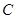 处有一电视塔,火车站正东方向的
处有一电视塔,火车站正东方向的 处有一小汽车,测得
处有一小汽车,测得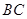 距离为31
距离为31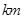 ,该小汽车从
,该小汽车从 处以60公里每小时的速度前往火车站,20分钟后到达
处以60公里每小时的速度前往火车站,20分钟后到达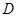 处,测得离电视塔21
处,测得离电视塔21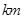 ,问小汽车到火车站还需多长时间?
,问小汽车到火车站还需多长时间?