(本小题满分9分)如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=a.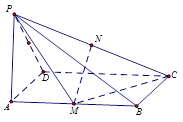
(1)求证:MN∥平面PAD;
(2)求证:平面PMC⊥平面PCD.
已知:函数 对一切实数
对一切实数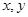 都有
都有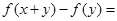
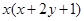 成立,且
成立,且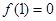 .
.
(1)求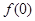 的值;
的值;
(2)求 的解析式。
的解析式。
(3)已知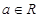 ,设P:当
,设P:当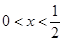 时,不等式
时,不等式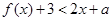 恒成立;Q:当
恒成立;Q:当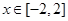 时,
时,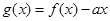 是单调函数。如果满足使P成立的
是单调函数。如果满足使P成立的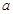 的集合记为
的集合记为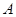 ,满足使Q成立的
,满足使Q成立的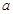 的集合记为
的集合记为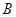 ,求
,求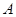 ∩
∩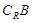 (
(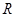 为全集)。
为全集)。
.已知函数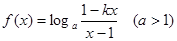 是奇函数
是奇函数
(1)求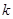 的值,并求出该函数的定义域;
的值,并求出该函数的定义域;
(2)根据(1)的结果,判断 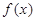 在
在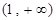 上的单调性,并给出证明.
上的单调性,并给出证明.
已知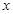
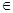 [
[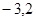 ],求函数
],求函数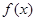 =
=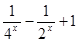 的最大值与最小值.
的最大值与最小值.
(本题满分10分) 选修4-5:不等式选讲
(Ⅰ)解关于x的不等式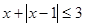 ;
;
(Ⅱ)若关于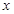 的不等式
的不等式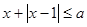 有解,求实数
有解,求实数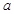 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是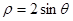 ,设直线
,设直线 的参数方程是
的参数方程是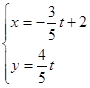 (
(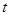 为参数)。
为参数)。
(Ⅰ)将曲线C的极坐标方程转化为直角坐标方程;
(Ⅱ)设直线 与
与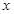 轴的交点是M,N为曲线C上一动点,求|MN|的最大值。
轴的交点是M,N为曲线C上一动点,求|MN|的最大值。