(本小题满分10分)如图,直角梯形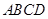 中,
中,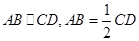 ,
, ,平面
,平面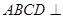 平面
平面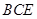 ,
, 为等边三角形,
为等边三角形, 分别是
分别是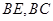 的中点,
的中点,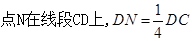 .
.
(1)证明:
 ;
;
(2)证明: 平面
平面 ;
;
(3)若 ,求几何体
,求几何体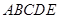 的体积.
的体积.
已知函数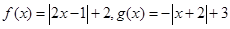
(1)解不等式: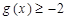 ;
;
(2)若关于x的不等式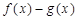 ≥m+2的解集为R,求实数m的取值范围.
≥m+2的解集为R,求实数m的取值范围.
已知函数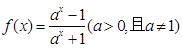 ,设函数
,设函数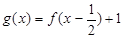
(1)求证: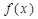 是奇函数;
是奇函数;
(2)①求证: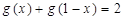 ;
;
②结合①的结论求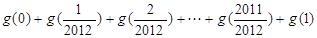 的值;
的值;
(3)仿上,设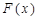 是
是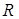 上的奇函数,请你写出一个函数
上的奇函数,请你写出一个函数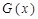 的解析式,并根据第(Ⅱ)问的结论,猜想函数
的解析式,并根据第(Ⅱ)问的结论,猜想函数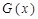 满足的一般性结论.
满足的一般性结论.
抛物线 的焦点为
的焦点为 ,
,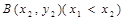 在抛物线上,
在抛物线上,
(1)存在实数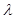 ,使
,使 ,求直线
,求直线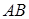 的方程;
的方程;
( 2 )以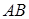 为直径的圆过
为直径的圆过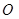 点,证
点,证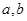 明直线
明直线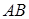 过定点,并求出定点坐标.
过定点,并求出定点坐标.
如图,斜三棱柱ABC—A1B1C1的底面是直角三角形,AC⊥CB,
∠ABC=45°,侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E、F分别是AB1、BC的中点.
(1)求证EF//平面A1ACC1;
(2)求EF与侧面A1ABB1所成的角;
(3)求二面角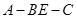 的大小的余弦值.
的大小的余弦值.
下表是关于宿州市服装机械厂某设备的使用年限(年)和所需要的维修费用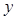 (万元)的几组统计数据:
(万元)的几组统计数据:
| 2 |
3 |
4 |
5 |
6 |
|
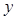 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
(1)请根据上表提供的数据,用最小二乘法求出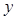 关于的线性回归方程;
关于的线性回归方程;
(2)估计使用年限为10年时,维修费用为多少?
(参考:①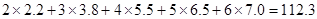
② )
)